It seems that LaTeX is currently experiencing some sort of issue that is preventing users from seeing particular input.
A temporary solution to this (if you're using a PC) is to right-click on the

icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).
The following message may appear:
This is due to the fact that the certificate for latex.codecogs.com has expired and needs to be updated. However, because the "Open image in new tab" option will only take you to an image file, there is most likely no real risk associated with proceeding, which can be done by clicking the "Advanced" button and then clicking on the "Proceed to latex.codecogs.com (unsafe)" option.
It is possible that the expired certificate of
https://latex.codecogs.com/ is what is causing this issue.
Alternatively, you may wish to wait until
https://latex.codecogs.com/ update their certificate, which will likely rectify the LaTeX issue on here.
. This can be done by noting that
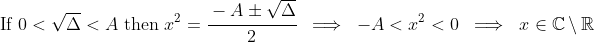
 icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).
icon, then clicking on "Open image in new tab" (for Google Chrome and Edge, or the equivalent option on other browsers).
