But
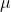
is a characteristic of the surface; a rough surface will have a higher value than a smoother one. It's value is found empirically, I'd imagine.
There are also the coeff. of static friction and the coeff. of kinetic friction, if this rusty brain of mine remembers correctly. They are supposed to differ.
Edit
On reflection, the friction between 2 surfaces ought to be a function of the coeffs. of both surfaces rather than that of the 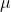 of one surface alone. Wonder what the actual facts are. Must be well-established by now.
of one surface alone. Wonder what the actual facts are. Must be well-established by now.
Just to add to that, as long as the car is travelling in a circle, it is the coefficient of
static friction that is operating.
But the moment that the car begins to slide, the coefficient of
kinetic friction takes over.
But the coefficient of kinetic friction is lower than the coefficient of static friction.
This means that what Integrand said before is not
quite right. The car would slide out to a radius at which the coefficient of
kinetic friction is just enough to supply the centripetal force. This radius is greater than that suggested by the coefficient of static friction. So when the car stops sliding and static friction again takes over, the greatest possible value of static friction is not being supplied. Which means that there is some leeway for the car to speed up without sliding.
Also, I'm not sure if "the friction between 2 surfaces ought to be a function of the coeffs. of both surfaces" is correct. The coefficient of friction is a value that already depends on the properties of both surfaces in contact. I don't think it is meaningful to talk of the coefficient of friction of say bitumen. It is like one hand clapping. But there would be a coefficient of friction for bitumen in contact with rubber, and another one for when this surface is lubricated with water. I doubt there is some generic function you could apply to the coefficients of each surface (if they existed) to get the combined coefficient. But I haven't looked it up, so I am prepared to be corrected.

