MX2 Integration Marathon (1 Viewer)

sharky564 · Oct 13, 2019

Another problem if u get bored of that one:

$\displaystyle \int_0^1 \frac{\ln(x+1)}{x} \; \mathrm{d}x = \frac{\pi^2}{12}$

No using dilogarithms, only 4U stuff.

stupid_girl · Oct 15, 2019

sharky564 said:
Another problem if u get bored of that one:

$\displaystyle \int_0^1 \frac{\ln(x+1)}{x} \; \mathrm{d}x = \frac{\pi^2}{12}$

No using dilogarithms, only 4U stuff.

Please correct me if there is any typo.
$\frac{1}{1+r}=\sum_{n=0}^{\infty}\left(-r\right)^{n}$
$\int_{0}^{x}\frac{1}{1+r}dr=\int_{0}^{x}\sum_{n=0}^{\infty}\left(-r\right)^{n}dr$
$\ln\left(1+x\right)=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n+1}}{n+1}$
$\frac{\ln\left(1+x\right)}{x}=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n}}{n+1}$
$\int_{0}^{1}\frac{\ln\left(1+x\right)}{x}dx=\int_{0}^{1}\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n}}{n+1}dx$
$=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}}{\left(n+1\right)^{2}}$
$=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n^{2}}$
$=\frac{\pi^{2}}{12}$

stupid_girl · Oct 15, 2019

sharky564 said:
That's what I like about this question - due to the simplicity of the q, there seem to be so many ways of approaching it which don't go anywhere

Do you have more hints?

sharky564 · Oct 16, 2019

stupid_girl said:
Please correct me if there is any typo.
$\frac{1}{1+r}=\sum_{n=0}^{\infty}\left(-r\right)^{n}$
$\int_{0}^{x}\frac{1}{1+r}dr=\int_{0}^{x}\sum_{n=0}^{\infty}\left(-r\right)^{n}dr$
$\ln\left(1+x\right)=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n+1}}{n+1}$
$\frac{\ln\left(1+x\right)}{x}=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n}}{n+1}$
$\int_{0}^{1}\frac{\ln\left(1+x\right)}{x}dx=\int_{0}^{1}\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}x^{n}}{n+1}dx$
$=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}}{\left(n+1\right)^{2}}$
$=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n^{2}}$
$=\frac{\pi^{2}}{12}$

I mean, you have to show why that sum is $\frac{\pi^2}{12}$ , but there are many ways of doing that in 4U, so it's basically done. That was also my method

.

sharky564 · Oct 16, 2019

stupid_girl said:
Do you have more hints?

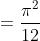
After a partial evaluation of the integral, you should get the original integral, which you can use for symmetry. See how that's possible. (note that this is quite cancerous to do, so you need to have some persistence)

stupid_girl · Oct 16, 2019

A few more alternative expressions that look interesting but not leading to a solution

$\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(\frac{\sec x-\cos x}{2}\right)dx$
$\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(\frac{\sin x\tan x}{2}\right)dx$
$\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(\frac{\sec x-\sin x}{1+\tan x}\right)dx$
$\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(\frac{1-\sin x\cos x}{\sin x+\cos x}\right)dx$
$\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(\sin x+\cos x-\frac{3\sin x}{1+\tan x}\right)dx$

stupid_girl · Oct 17, 2019

Some more interesting expressions but no success
$\int_{0}^{\frac{\pi}{4}}\tan^{-1}\left(\frac{1-\sin x\cos x}{\sin x+\cos x}\right)dx$
$\int_{0}^{\frac{\pi}{4}}\tan^{-1}\left(\frac{2-\cos2x}{2\sqrt{2}\cos x}\right)dx$
$\int_{0}^{\frac{\pi}{4}}\tan^{-1}\left(\frac{1+2\sin^{2}x}{2\sqrt{2}\cos x}\right)dx$
$\int_{0}^{\frac{\pi}{4}}\tan^{-1}\left(\frac{3\sec x-2\cos x}{2\sqrt{2}}\right)dx$

@sharky564 I wanna give up. How did you solve this integral?

stupid_girl · Oct 18, 2019

I have decided to give up @sharky564 question.

This is a new question that should be solvable in 4U.
$$Given that $\int_{0}^{\infty}\frac{1}{1+x^{k}}dx=\frac{\pi}{k}\csc\frac{\pi}{k}$ for $k>1$. Find $\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{\pi-1}+\left(1-\sin\sqrt{x}\right)^{\pi-1}}{\left(1+\sin\sqrt{x}\right)^{\pi}+\left(1-\sin\sqrt{x}\right)^{\pi}}dx$.$

stupid_girl · Oct 19, 2019

One more question
$\lim_{n\to\infty} \int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
(It can be solved without knowing the result in #217.

)

stupid_girl · Oct 20, 2019

This question can take ages if you're not on the right track.

$\frac{\int_{0}^{1}\left(1+a+b+c\right)^{m}x^{n}dx}{\int_{0}^{1}\log_{2}\left(\sqrt[n+1]{\frac{\left(16^{\sqrt{x}}+k\cdot4^{\sqrt{x}}+4\right)\left(16^{1-\sqrt{x}}+k\cdot4^{1-\sqrt{x}}+4\right)\left(\sec^{2}\frac{\pi x}{4}+2\tan\frac{\pi x}{4}\right)^{a}}{\left(4^{\sqrt{x}}+k\cdot2^{\sqrt{x}}+4\right)\left(4^{1-\sqrt{x}}+k\cdot2^{1-\sqrt{x}}+4\right)\left(\sin\frac{\pi x}{2}\right)^{b}\left(\cos\frac{\pi x}{2}\right)^{c}}}\right)dx}=\left(1+a+b+c\right)^{m-1}$
(modified to make it look more evil

...feel free to share your attempt)

HeroWise · Oct 22, 2019

why does Sharkys Integral look much easier compared to that

stupid_girl · Oct 22, 2019

HeroWise said:
why does Sharkys Integral look much easier compared to that

It's difficult to judge the difficulty from appearance. sqrt(tan x) may look simple but it's more tedious to integrate than some horrible looking functions.

stupid_girl · Oct 25, 2019

stupid_girl said:
One more question
$\lim_{n\to\infty} \int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
(It can be solved without knowing the result in #217.)

$\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
$=2\int_{0}^{\pi}u\frac{\left(1+\sin u\right)^{n}+\left(1-\sin u\right)^{n}}{\left(1+\sin u\right)^{n+1}+\left(1-\sin u\right)^{n+1}}du\ \left(Let\ u=\sqrt{x}\right)$
$=2\int_{0}^{\frac{\pi}{2}}\left(u+\pi-u\right)\frac{\left(1+\sin u\right)^{n}+\left(1-\sin u\right)^{n}}{\left(1+\sin u\right)^{n+1}+\left(1-\sin u\right)^{n+1}}du$
$=2\pi\int_{0}^{\frac{\pi}{2}}\frac{\left(1+\sin u\right)^{n}+\left(1-\sin u\right)^{n}}{\left(1+\sin u\right)^{n+1}+\left(1-\sin u\right)^{n+1}}du$
$=2\pi\int_{0}^{\frac{\pi}{2}}\frac{\left(1+\cos v\right)^{n}+\left(1-\cos v\right)^{n}}{\left(1+\cos v\right)^{n+1}+\left(1-\cos v\right)^{n+1}}dv\left(Let\ v=\frac{\pi}{2}-u\right)$
$=2\pi\int_{0}^{1}\frac{\left(1+\frac{1-t^{2}}{1+t^{2}}\right)^{n}+\left(1-\frac{1-t^{2}}{1+t^{2}}\right)^{n}}{\left(1+\frac{1-t^{2}}{1+t^{2}}\right)^{n+1}+\left(1-\frac{1-t^{2}}{1+t^{2}}\right)^{n+1}}\cdot\frac{2}{1+t^{2}}dt\left(Let\ t=\tan\frac{v}{2}\right)$
$=2\pi\int_{0}^{1}\frac{\left(\frac{2}{1+t^{2}}\right)^{n}+\left(\frac{2t^{2}}{1+t^{2}}\right)^{n}}{\left(\frac{2}{1+t^{2}}\right)^{n+1}+\left(\frac{2t^{2}}{1+t^{2}}\right)^{n+1}}\cdot\frac{2}{1+t^{2}}dt$
$=2\pi\int_{0}^{1}\frac{\left(1+t^{2n}\right)\left(\frac{2}{1+t^{2}}\right)^{n}}{\left(1+t^{2n+2}\right)\left(\frac{2}{1+t^{2}}\right)^{n+1}}\cdot\frac{2}{1+t^{2}}dt$
$=2\pi\int_{0}^{1}\frac{1+t^{2n}}{1+t^{2n+2}}dt$

Taking limit
$\lim_{n\to\infty} \int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
$=\lim_{n\to\infty} 2\pi\int_{0}^{1}\frac{1+t^{2n}}{1+t^{2n+2}}dt$
$=2\pi\int_{0}^{1}\lim_{n\to\infty}\frac{1+t^{2n}}{1+t^{2n+2}}dt$
$=2\pi\int_{0}^{1}dt$
$=2\pi$

stupid_girl · Oct 25, 2019

stupid_girl said:
I have decided to give up @sharky564 question.

This is a new question that should be solvable in 4U.
$$Given that $\int_{0}^{\infty}\frac{1}{1+x^{k}}dx=\frac{\pi}{k}\csc\frac{\pi}{k}$ for $k>1$. Find $\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{\pi-1}+\left(1-\sin\sqrt{x}\right)^{\pi-1}}{\left(1+\sin\sqrt{x}\right)^{\pi}+\left(1-\sin\sqrt{x}\right)^{\pi}}dx$.$

Continuing from above
$\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
$=2\pi\int_{0}^{1}\frac{1+t^{2n}}{1+t^{2n+2}}dt$
$=2\pi\int_{0}^{1}\frac{1}{1+t^{2n+2}}dt-\int_{0}^{1}\frac{-t^{-2}}{t^{-2n-2}+1}dt$
$=2\pi\int_{0}^{1}\frac{1}{1+t^{2n+2}}dt-\int_{\infty}^{1}\frac{1}{s^{2n-2}+1}dt\left (Let\ t=\frac{1}{s}\right)$
$=2\pi\int_{0}^{\infty}\frac{1}{1+t^{2n+2}}dt$
$=2\pi\cdot\frac{\pi}{2n+2}\csc\frac{\pi}{2n+2}$
$=\frac{\pi^{2}}{n+1}\csc\frac{\pi}{2n+2}$

Put $n=\pi-1$
$\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{\pi-1}+\left(1-\sin\sqrt{x}\right)^{\pi-1}}{\left(1+\sin\sqrt{x}\right)^{\pi}+\left(1-\sin\sqrt{x}\right)^{\pi}}dx$
$=\frac{\pi^{2}}{\pi}\csc\frac{\pi}{2\pi}$
$=\pi\csc\frac{1}{2}$

It's also easy to verify the limiting case.
$\lim_{n\to\infty}\int_{0}^{\pi^{2}}\frac{\left(1+\sin\sqrt{x}\right)^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx$
$=\lim_{n\to\infty}\frac{\pi^{2}}{n+1}\csc\frac{\pi}{2n+2}$
$=2\pi\lim_{n\to\infty}\frac{\frac{\pi}{2n+2}}{\sin\frac{\pi}{2n+2}}$
$=2\pi\lim_{m\to 0}\frac{m}{\sin m}\left (Let\ m=\frac{\pi}{2n+2}\right)$
$=2\pi$

stupid_girl · Oct 26, 2019

Thanks God! I finally have a way out for @sharky564 integral. I will try to type the solution over the weekend.

stupid_girl · Oct 26, 2019

$\int\frac{x\cos x}{1+\sin^{2}x}dx$
$=x\tan^{-1}\left(\sin x\right)-\int\tan^{-1}\left(\sin x\right)dx$

Let's try Feynman trick.
$I\left(a\right)=\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(a\sin x\right)dx$
$I'\left(a\right)=\int_{0}^{\frac{\pi}{2}}\frac{\sin x}{1+\left(a\sin x\right)^{2}}dx$
$\int_{0}^{\frac{\pi}{2}}\frac{\sin x}{1+a^{2}\left(1-\cos^{2}x\right)}dx$
$=\int_{1}^{0}\frac{-1}{1+a^{2}\left(1-t^{2}\right)}dt$ (Let t=cos x)
$=\int_{1}^{0}\frac{1}{\left(at+\sqrt{1+a^{2}}\right)\left(at-\sqrt{1+a^{2}}\right)}dt$
$=\frac{1}{2a\sqrt{1+a^{2}}}\int_{1}^{0}\left(\frac{1}{t-\frac{\sqrt{1+a^{2}}}{a}}-\frac{1}{t+\frac{\sqrt{1+a^{2}}}{a}}\right)dt$
$=\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}$

$I\left(1\right)-I\left(0\right)=\int_{0}^{1}\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}da$
Note that I(0)=0 and let
$u=a+\sqrt{1+a^{2}}$
$a=\frac{u^{2}-1}{2u}$

$I\left(1\right)=\int_{0}^{1}\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}da$
$=\int_{1}^{1+\sqrt{2}}\frac{2\ln u}{u^{2}-1}du$
$=\int_{1}^{1+\sqrt{2}}\left(\frac{\ln u}{u-1}-\frac{\ln u}{u+1}\right)du$

This will unfortunately lead to dilogarithm but at least this is a way out. I will be extremely impressed if someone can provide a solution using 4U methods.

sharky564 · Oct 27, 2019

stupid_girl said:
$\int\frac{x\cos x}{1+\sin^{2}x}dx$
$=x\tan^{-1}\left(\sin x\right)-\int\tan^{-1}\left(\sin x\right)dx$

Let's try Feynman trick.
$I\left(a\right)=\int_{0}^{\frac{\pi}{2}}\tan^{-1}\left(a\sin x\right)dx$
$I'\left(a\right)=\int_{0}^{\frac{\pi}{2}}\frac{\sin x}{1+\left(a\sin x\right)^{2}}dx$
$\int_{0}^{\frac{\pi}{2}}\frac{\sin x}{1+a^{2}\left(1-\cos^{2}x\right)}dx$
$=\int_{1}^{0}\frac{-1}{1+a^{2}\left(1-t^{2}\right)}dt$ (Let t=cos x)
$=\int_{1}^{0}\frac{1}{\left(at+\sqrt{1+a^{2}}\right)\left(at-\sqrt{1+a^{2}}\right)}dt$
$=\frac{1}{2a\sqrt{1+a^{2}}}\int_{1}^{0}\left(\frac{1}{t-\frac{\sqrt{1+a^{2}}}{a}}-\frac{1}{t+\frac{\sqrt{1+a^{2}}}{a}}\right)dt$
$=\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}$

$I\left(1\right)-I\left(0\right)=\int_{0}^{1}\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}da$
Note that I(0)=0 and let
$u=a+\sqrt{1+a^{2}}$
$a=\frac{u^{2}-1}{2u}$

$I\left(1\right)=\int_{0}^{1}\frac{\ln\left(a+\sqrt{1+a^{2}}\right)}{a\sqrt{1+a^{2}}}da$
$=\int_{1}^{1+\sqrt{2}}\frac{2\ln u}{u^{2}-1}du$
$=\int_{1}^{1+\sqrt{2}}\left(\frac{\ln u}{u-1}-\frac{\ln u}{u+1}\right)du$

This will unfortunately lead to dilogarithm but at least this is a way out. I will be extremely impressed if someone can provide a solution using 4U methods.

That last section which results in a dilogarithm is entirely 4U-able, and you may see that if you try the Feynman in a slightly different way.

sharky564 · Nov 3, 2019

akkjen · Nov 3, 2019

sharky564 said:
$\displaystyle \int_0^{\frac{\pi}{2}} \dfrac{\ln \left ( a^2 \sin^2 (x) + b^2 \cos^2 (x) \right )}{a^2 \sin^2 (x) + b^2 \cos^2 (x)} \; \mathrm{d}x = \dfrac{\pi}{ab} \ln \left ( \dfrac{2ab}{a + b} \right )$

17

stupid_girl · Nov 3, 2019

I'll try @sharky564 question later.

This question should be more accessible to 4U students.

$\int_{0}^{\frac{\pi}{4}}\left(\tan x-\tan^{2}x\right)^{4}dx$

MX2 Integration Marathon (1 Viewer)

Member

Active Member

Active Member

Member

Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

Member

Member

Active Member

Active Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)