Doesn't look like you were bored of maths considering you got a 99 for 4U. There had to be some interest there lolIt does look like it doesn’t it! Jkjk
In reality, I really only like integration now because there is a certain elegance to it and skill required (and it’s still fresh in my head). I find the rest of maths quite boring and stale imho. My attempts at the above integrals are really just due to boredom (not long till uni starts now though).
-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MX2 Integration Marathon (1 Viewer)
- Thread starter dan964
- Start date
This can easily be converted to a much more recognisable integral with the substitution:The ultimate tedious integral:
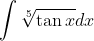
From which it follows that:
and the problem is reduced to a very (very) messy partial fractions problem. According to the integral calculator, and after cleaning up its awful formatting / presentation, the indefinite integral is:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I wrote this in the past but I have now forgotten how to solve it.
\left(16^{1-\sqrt{x}}+k\cdot4^{1-\sqrt{x}}+4\right)}{\left(4^{\sqrt{x}}+k\cdot2^{\sqrt{x}}+4\right)\left(4^{1-\sqrt{x}}+k\cdot2^{1-\sqrt{x}}+4\right)}\right)dx=1)
Edit: I remember how to solve it now.
Edit: I remember how to solve it now.
Last edited:
Is the question here to prove this result - i.e. that the integral is 1 irrespective of the value of k - or is this an equation that needs to be solved to find the value(s) of k?I wrote this in the past but I have now forgotten how to solve it.
\left(16^{1-\sqrt{x}}+k\cdot4^{1-\sqrt{x}}+4\right)}{\left(4^{\sqrt{x}}+k\cdot2^{\sqrt{x}}+4\right)\left(4^{1-\sqrt{x}}+k\cdot2^{1-\sqrt{x}}+4\right)}\right)dx=1)
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
The integral is 1 irrespective of the value of k.Is the question here to prove this result - i.e. that the integral is 1 irrespective of the value of k - or is this an equation that needs to be solved to find the value(s) of k?
can you post the solution here? This gives me a headache for the last few daysI wrote this in the past but I have now forgotten how to solve it.
Edit: I remember how to solve it now.
Yeah lol, some factoring trick I imagine, or King Rule but I dont see how that is used.can you post the solution here? This gives me a headache for the last few days
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
What tricks have you tried?can you post the solution here? This gives me a headache for the last few days
The following techniques are NOT required.
integration by parts
differentiation under the integral sign
hyperbolic function
I've tried all the techniques above. I think the problem will be solved by substituting x with another variable t and we got I + I = 2 so I = 1.What tricks have you tried?
The following techniques are NOT required.
integration by parts
differentiation under the integral sign
hyperbolic function
Am i on the right path?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
By adjusting the coefficient of k to 1, you should be able to take out log_2 (2), which is just 1. Integrating dx from 0 to 1 gives you 1.
The remaining factors have the same structure and you can offset them by suitable substitution.
The remaining factors have the same structure and you can offset them by suitable substitution.
if ur stupid, what am i.By adjusting the coefficient of k to 1, you should be able to take out log_2 (2), which is just 1. Integrating dx from 0 to 1 gives you 1.
The remaining factors have the same structure and you can offset them by suitable substitution.
F
Paradoxica
-insert title here-
Define
 := \log_a\left(a^{u} + k + a^{v}\right))
The original question takes the argument a=2.
For brevity, we will suppress the first two arguments⁰, as it turns out they are irrelevant to the final answer.
(This is a thing in higher mathematics lmao get used to it)
The original question is equivalent¹ to:
+\psi\left(2-2\sqrt{x},2\sqrt{x}\right)- \psi\left(\sqrt{x},2-\sqrt{x}\right) - \psi\left(1-\sqrt{x},1+\sqrt{x}\right) + \nolinebreak 1 \right) \mathrm{d}x)
It is clear that ψ(u,v) = ψ(v,u), from the definition, so we can collapse the first two terms together.
Break off the +1 term and ignore it for now, as that is what gives the final answer.
Using the substitution x = t², the integral becomes:
 - \psi\left(t,2-t\right) - \psi\left(1+t,1-t\right) \right) t \mathrm{d}t)
Using the boundary preserving transformation t→1-t, this becomes:
 - \psi\left(1-t,1+t\right) - \psi\left(2-t,t\right) \right) (1-t) \mathrm{d}t)
Use symmetry in u,v, once again, to reorder the arguments to be the same as before.
Take the average of this and the previous step, to obtain:
 - \psi\left(t,2-t\right) - \psi\left(1+t,1-t\right) \right) \mathrm{d}t)
We consider only the last two terms for now.
Define:
 \mathrm{d}t; \quad B := \int_0^1 \psi\left(1+t,1-t\right) \mathrm{d}t)
By the same boundary preserving transformation as before, it is obvious that A = B.
Use the scaling transformation t→2t:
 \mathrm{d}t)
Use the same "boundary preserving transformation" to change the interval [0,½] → [½,1]
 \mathrm{d}t = 2\int_{\frac{1}{2}}^1 \psi\left(2t,2-2t\right) \mathrm{d}t)
Finally, we have:
 \mathrm{d}t = \int_0^1 2\psi\left(2t,2-2t\right) \mathrm{d}t)
Returning to the step before we defined A and B, we obtain:
 \mathrm{d}t -(A+B) = \int_0^1 2\psi\left(2t,2-2t\right)-2\psi\left(2t,2-2t\right) \mathrm{d}t = 0)
The +1 term is trivially integrated to obtain 1, which is the final answer.
⁰ ψ(u,v) = ψ(a,k,u,v)
¹ left as an exercise to the reader
The original question takes the argument a=2.
For brevity, we will suppress the first two arguments⁰, as it turns out they are irrelevant to the final answer.
(This is a thing in higher mathematics lmao get used to it)
The original question is equivalent¹ to:
It is clear that ψ(u,v) = ψ(v,u), from the definition, so we can collapse the first two terms together.
Break off the +1 term and ignore it for now, as that is what gives the final answer.
Using the substitution x = t², the integral becomes:
Using the boundary preserving transformation t→1-t, this becomes:
Use symmetry in u,v, once again, to reorder the arguments to be the same as before.
Take the average of this and the previous step, to obtain:
We consider only the last two terms for now.
Define:
By the same boundary preserving transformation as before, it is obvious that A = B.
Use the scaling transformation t→2t:
Use the same "boundary preserving transformation" to change the interval [0,½] → [½,1]
Finally, we have:
Returning to the step before we defined A and B, we obtain:
The +1 term is trivially integrated to obtain 1, which is the final answer.
⁰ ψ(u,v) = ψ(a,k,u,v)
¹ left as an exercise to the reader
Last edited:
Paradoxica
-insert title here-
the real answer to this conundrum is that by using a substitution which maps a finite open interval to ℝ, you cannot invert the substitution to obtain an antiderivative valid over all of ℝ. the substitution is only bijective locally, not globally, so a true inverse does not exist, hence the antiderivative is only valid over specific subsets of ℝ. in order to obtain an antiderivative that is valid on all of ℝ, you need a different method.
more to read here:
more to read here:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Let
From derivative calc:
No clue how to do the second integral.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
You choose the correct substitution but calculate du/dx incorrectly.Let
From derivative calc:
No clue how to do the second integral.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
By the way, choosing the correct substitution is not the end of story.
Remember to split the interval.
}{x^{4}+x^{2}\sin\left(4\ln x\right)+\cos^{2}\left(2\ln x\right)}dx=\int_{1}^{e^{\frac{\pi}{4}}}\frac{x^{3}-x\cos^{2}\left(2\ln x\right)}{x^{4}+x^{2}\sin\left(4\ln x\right)+\cos^{2}\left(2\ln x\right)}dx+\int_{e^{\frac{\pi}{4}}}^{e^{\frac{3\pi}{4}}}\frac{x^{3}-x\cos^{2}\left(2\ln x\right)}{x^{4}+x^{2}\sin\left(4\ln x\right)+\cos^{2}\left(2\ln x\right)}dx+\int_{e^{\frac{3\pi}{4}}}^{e^{\frac{5\pi}{4}}}\frac{x^{3}-x\cos^{2}\left(2\ln x\right)}{x^{4}+x^{2}\sin\left(4\ln x\right)+\cos^{2}\left(2\ln x\right)}dx+\int_{e^{\frac{5\pi}{4}}}^{100}\frac{x^{3}-x\cos^{2}\left(2\ln x\right)}{x^{4}+x^{2}\sin\left(4\ln x\right)+\cos^{2}\left(2\ln x\right)}dx)
If you are wondering how these break points are chosen, you may try to graph}}{x^2}\right)) .
.
If you are wondering how these break points are chosen, you may try to graph
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Last edited:
