Need helps pls (1 Viewer)
- Thread starter =)(=
- Start date
yanujw
Well-Known Member
- Joined
- May 23, 2020
- Messages
- 339
- Gender
- Male
- HSC
- 2022
Consider the fact that when a function is squared, each point on the function is squared vertically, since the y-axis is the output of a function.
For every point) the new point is
the new point is ) , where y≥0
, where y≥0
If a HA is at y=3 for example, in the root function it is at the square root of that, so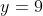
However if a VA is at x=3, you can't take a square of a function at a point where it doesn't exist, so the asymptote remains. The values that make the original value undefined, are the same that make the squared function undefined.
For every point
If a HA is at y=3 for example, in the root function it is at the square root of that, so
However if a VA is at x=3, you can't take a square of a function at a point where it doesn't exist, so the asymptote remains. The values that make the original value undefined, are the same that make the squared function undefined.
So its basically that you are square rooting the vertical components of the function while not changing the horizontal components meaning the horizontal position isn't changed?Consider the fact that when a function is squared, each point on the function is squared vertically, since the y-axis is the output of a function.
For every pointthe new point is
, where y≥0
If a HA is at y=3 for example, in the root function it is at the square root of that, so
However if a VA is at x=3, you can't take a square of a function at a point where it doesn't exist, so the asymptote remains. The values that make the original value undefined, are the same that make the squared function undefined.
Suppose we have functions ) and
and 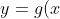) where
where 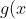=\sqrt{f(x)}) .
.
Vertical asymptotes of) could occur when
could occur when ) is undefined.
is undefined.
Vertical asymptotes on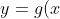=\sqrt{f(x)}) mean looking for where
mean looking for where 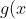) is undefined, and that means considering both
is undefined, and that means considering both
=0) ) will become end points rather than asymptotes as
) will become end points rather than asymptotes as 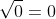 and is thus well-defined.
and is thus well-defined.
Horizontal asymptotes are found by examining the beahaviour of a function as a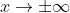 .
.
 \to C\ \text{as}\ x \to +\infty\ \text{(say), then}\ g(x) = \sqrt{f(x)} \to \sqrt{C}.)
In your specific case:
 = 2 + \cfrac{1}{x+2} \qquad \qquad \text{and} \qquad \qquad g(x) = \sqrt{f(x)} = \sqrt{2 +\cfrac{1}{x+2}})
As every real constant except zero has a reciprocal, it is clear that) is only undefined if
is only undefined if 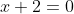 and thus the domain of
and thus the domain of \ \text{is}\ \left\{x \in \mathbb{R},\ x \ne -2\right\}) and that
and that 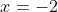 is a vertical asymptote because:
is a vertical asymptote because:
 \to +\infty.)
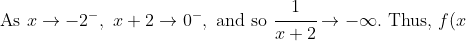 \to -\infty.)
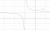
And, the result is a typical rectangular hyperbola with the asymptotes shifted to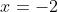 and
and 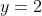 (shown as green dotted lines).
(shown as green dotted lines).
Now, for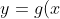) , the domain requires
, the domain requires  \geqslant 0) and so the part of
and so the part of ) below the
below the  -axis will be outside the domain of
-axis will be outside the domain of 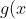) . The domain of
. The domain of 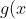) is thus:
is thus:
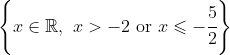
The  -intercept of
-intercept of ) , at
, at 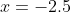 , will remain a zero for
, will remain a zero for 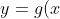) but it also becomes an end point, and one with a vertical tangent as
but it also becomes an end point, and one with a vertical tangent as
 = \sqrt{f(x)} =\big[f(x)\big]^{\frac{1}{2}} \qquad \implies \qquad g'(x) &= \cfrac{1}{2}\big[f(x)\big]^{-\frac{1}{2}} \times f'(x) \qquad \text{(Chain Rule)} \\ &= \cfrac{f'(x)}{2\sqrt{f(x)}} \qquad \text{which is undefined for $f(x)=0$ provided $f'(x) \ne 0$} \end{align*})
There will remain a vertical asymptote at 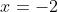 as
as 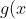) is undefined there. The horizontal asymptote will shift to
is undefined there. The horizontal asymptote will shift to 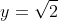 as
as  \to 2 \implies g(x) = \sqrt{f(x)} \to \sqrt{2}) .
.
The curve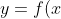) will lie above
will lie above 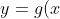) wherever
wherever  > 1) as the square root of any value greater than 1 produces a smaller number (for example,
as the square root of any value greater than 1 produces a smaller number (for example, 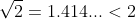 ).
).
The two curves will meet only when = 0) of
of  = 1) as 0 and 1 are the only two numbers that are there own square root. The intersections are thus
as 0 and 1 are the only two numbers that are there own square root. The intersections are thus ) and
and ) .
.
The curve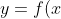) will lie below
will lie below 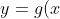) wherever
wherever 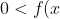 < 1) as the square root of any positive value less than 1 produces a greater number (for example,
as the square root of any positive value less than 1 produces a greater number (for example, 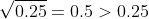 ).
).
The results from plotting the curves is shown below, matching the above description. The new asymptote at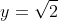 has been added as a purple dotted line.
has been added as a purple dotted line.

Vertical asymptotes of
Vertical asymptotes on
- anywhere that
(as outside the domain of
)
- as well as anywhere that
is undefined.
Horizontal asymptotes are found by examining the beahaviour of a function as a
In your specific case:
As every real constant except zero has a reciprocal, it is clear that
And, the result is a typical rectangular hyperbola with the asymptotes shifted to

Now, for
The curve
The two curves will meet only when
The curve
The results from plotting the curves is shown below, matching the above description. The new asymptote at

