Official BOS Trial 2015 Thread (4 Viewers)

[pororo]

Ah okay, so paradoxica is browsing this page atm, let's see if he knows how

 

[Carrotsticks]

does anyone know how to do question 15cii and iii?

For (c) (ii), sketch y=(x^2-1)/(x^2+1) and y=kx+1, and you can see no matter what K value you pick (other than k=0, which cannot be the case anyway) you will always have exactly one point of intersection. In other words always one real root. From this, you can also see that when K is large, the real root approaches 0 (will be used later).

For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.

 

[Paradoxica]

For (c) (ii), sketch y=(x^2-1)/(x^2+1) and y=kx+1, and you can see no matter what K value you pick (other than k=0, which cannot be the case anyway) you will always have exactly one point of intersection. In other words always one real root. From this, you can also see that when K is large, the real root approaches 0 (will be used later).

For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.

Oh. Well I substituted four values, namely, -1/k, 1, 0 and -1
P(-1/k) = 1-(1/k^2), P(1) = 2(k+1), P(0) = 2, P(-1) = 2(1-k)

We will now consider three cases for k.

Case 1: |k| < 1 means that P(-1/k) is negative. Combine with P(0) and there is a root by the intermediate value theorem.

Case 2: k < -1 means that P(1) is negative. Similar as above.

Case 3: k > 1 means that P(-1) is negative. Similar as above.

Degenerate cases occur if |k| = 1, as the root is trivial.

As you may have deduced already, I despise curve sketching.

 

[InteGrand]

Oh. Well I substituted four values, namely, -1/k, 1, 0 and -1
P(-1/k) = 1-(1/k^2), P(1) = 2(k+1), P(0) = 2, P(-1) = 2(1-k)

We will now consider three cases for k.

Case 1: |k| < 1 means that P(-1/k) is negative. Combine with P(0) and there is a root by the intermediate value theorem.

Case 2: k < -1 means that P(1) is negative. Similar as above.

Case 3: k > 1 means that P(-1) is negative. Similar as above.

Degenerate cases occur if |k| = 1, as the root is trivial.

As you may have deduced already, I despise curve sketching.

Alternatively, can just differentiate P and show that its derivative has no zeros so P is monotonic (and use the fact that P has at least one real root, being a cubic (follows from IVT), so it has exactly one root)). Neither of these methods really use part (i) though, unless you subbed your values in to the expression in part (i), or differentiated the expression in part (i), but these are trivial ways to "use" it.

 

[Paradoxica]

For (c) (iii) play around with sums and products of roots, and use the fact that the real root approaches zero to deduce the behavior of the modulus and argument. What ends up happening is that the non-real roots approach i and -i.

...OR you could just divide the entire cubic in it's reduced form by k, and letting k tend to infinity will degenerate the cubic into (x^2+1)x = 0

 

[Carrotsticks]

Alternatively, can just differentiate P and show that its derivative has no zeros so P is monotonic (and use the fact that P has at least one real root, being a cubic (follows from IVT), so it has exactly one root)). Neither of these methods really use part (i) though, unless you subbed your values in to the expression in part (i), or differentiated the expression in part (i), but these are trivial ways to "use" it.

Perhaps saying "Hence, or otherwise", would have been preferable.

...OR you could just divide the entire cubic in it's reduced form by k, and letting k tend to infinity will degenerate the cubic into (x^2+1)x = 0

This will find what the roots eventually become, but how would you then describe the behaviour of the roots as k varies? Part of the idea of the question was to get students to picture an 'animation' of what would happen to the roots as K gradually increases in value.

 

[Drsoccerball]

Is this Extension 1 or 2?

Extension 1.

 

[Carrotsticks]

Extension 1.

I admit Q12 was quite difficult.

However, I think Q14 is very reasonable.

Q14 (a) (i) can be done in two or three lines at most, with very little calculations (mostly explaining).

Q14 (a) (ii) is a little more difficult but it is implied that you simplify part (i) and take the sum of the simplified form.

It is unfamiliar though, you don't often see questions adding probabilities to prove binomial identities.

Q14 (b) and (c) are not difficult really (once you see the solution), but intimidating perhaps.

 

[Drsoccerball]

Theres no question 12 C ?
Was question 11d the result of newtons method of approximation ?

 

[RealiseNothing]

Theres no question 12 C ?
Was question 11d the result of newtons method of approximation ?

11d is pretty much the idea behind newtons method since you approximate roots using tangents.

 

[Mr_Kap]

Trebla/Carrotsticks

Do you think that the 2u Bos trial will be uploaded before the HSC maths exam? Because i might want to do the exam the day before the HSC math exam. If not, all good

 

[Paradoxica]

Q14 (b) and (c) are not difficult really (once you see the solution), but intimidating perhaps.

I rarely get intimidated. Frequently, however, I find myself flummoxed.

 

[anomalousdecay]

Did someone make origami during the papers lol? I spotted what looked like a crushed paper crane when cleaning at the end of the day.

 

[lita1000]

Can someone upload the papers?

 

[leehuan]

I was just scrolling.

Here's a question scrapped from 2U because it was too easy.

Hmm...



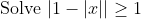
I'm curious, what was the trap?
____________________

My guesses are Simpsons rule/ trapezoidal rule or the AM-GM inequality

Wait. How did you know what Q16 was gonna be before when you were in there

 

[Drsoccerball]

I was just scrolling.



Hmm...



I'm curious, what was the trap?
____________________


Wait. How did you know what Q16 was gonna be before when you were in there

I think it would've been the fact that x=0 is a solution.

 

[Drsoccerball]

Wait. How did you know what Q16 was gonna be before when you were in there

 

[leehuan]

I think it would've been the fact that x=0 is a solution.

Dunno, I made it pop out on it's own.
________________________________

If youre as good as you are in integration i reckon you could state rank

It's supposed to be my best topic. I haven't gone into beyond HSC yet but I had 98% of 4U integration in the bag sometime during Year 11 lol

 

[leehuan]

I'm avoiding the perms and combs marathon LOL...

 

[Drsoccerball]

Page 1 of question 16 was to prove AM-GM second was with trap rule lol...