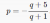-So it is given that QR ⟂ PR, hence mQRmPR=-1.
-After you find the gradients and simplify you should eventually get the condition pq + p + q = -5.
-Rearrange for p, and you get p=(-5-q)/(q+1)
-From the above it should be clear that q cannot equal -1 as the denominator of a fraction cannot equal zero
-Rearrange for q and you will end up with the same result that is p cannot equal -1
-Hence p and q cannot equal -1
Now p and q also cannot equal to 1 because if they did they would essentially become the point R (2a,a).
That is if p=1 the the point P(2ap, ap2) would become P(2a,a) which is the same is the point R. Same goes for q=1.
If p or q were to equal to one then PR and QR respectively would become points and not line segments. Which is just baloney!!
So in the end p and q cannot equal to plus/minus 1. Hope that helped!!
Note that is says
distinct points so that already implies

You can easily see that's true if you simply observe the equation m
QRm
PR=-1. which leads to (p+1)(q+1) = -4 and you'll understand that p and q can't be -1 as you'll get zero.
However also observe that both p+1 and q+1 can't be both positive (and likewise, can't be both negative)
This leads to the conclusion that if p<-1 , then q must be greater than -1 (or q can't be less than -1)
if p>-1 then q <-1 (or q can't be greater than -1)
If you observe the diagram, if p = -1, then PR would be a horizontal line. That implies that QR would have to be vertical line, which is impossible.
 ) and
and  ) lie on the parabola
lie on the parabola 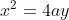 . The points
. The points  and
and  are constrained to move such that
are constrained to move such that  where
where  is the fixed point
is the fixed point  ) , which also lies on the parabola, given
, which also lies on the parabola, given  . By drawing the diagram, or otherwise, find the values of
. By drawing the diagram, or otherwise, find the values of  and
and  for which the relationship
for which the relationship  is not possible.
is not possible.