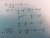Jackson94
Member
- Joined
- Jun 5, 2010
- Messages
- 44
- Gender
- Male
- HSC
- 2012
P and Q are the point t=p and t=q on the parabola x = 2at, y = at^2
a) Find the equations of the normals to the curve P and Q.
b) Prove that p^3 -q^3 = (p-q)(p^2 + pq + q^2)
Thanks in advance guys, obv part a is easy but you need it for part b I presume so I left it in.
a) Find the equations of the normals to the curve P and Q.
b) Prove that p^3 -q^3 = (p-q)(p^2 + pq + q^2)
Thanks in advance guys, obv part a is easy but you need it for part b I presume so I left it in.