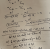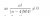-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
perms and combs question (1 Viewer)
- Thread starter banigul@30
- Start date
WeiWeiMan
Well-Known Member
Consider the combination formulahi, i need help with this question, i have already solved it up to a point but i don't know where to go with it, also i think there may be any easier way to solve it
any help is appreciated!
View attachment 42672
nCr = n!/r!(n-r!)
By inspection, n=6+4=10
banigul@30
Sleepy af
thank you!Consider the combination formula
nCr = n!/r!(n-r!)
By inspection, n=6+4=10
Each row of Pascal's Triangle has terms that are distributed symmetrically. In binomial coefficient form, this symmetry property can be expressed as:Consider the combination formula
nCr = n!/r!(n-r!)
By inspection, n=6+4=10\qquad
banigul@30
Sleepy af
thank you for this, this was the answer in the textbook! i tried using alegbra too but i made it too complicated hahaSome good answers were provided in this thread. Another approach is to brute force the answer by algebra;
... and solving this quadratic gives the solutions n=10 and n=-1, the latter is disregarded.
Attachments
-
1.7 MB Views: 18
Your algebra is correct, you got tothank you for this, this was the answer in the textbook! i tried using alegbra too but i made it too complicated haha
Last edited:
banigul@30
Sleepy af
Sure...i appreciate the help and the note on the second method, thank you!
could you explain View attachment 42676 thanks!