-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Polynomials question (1 Viewer)
- Thread starter enigma_1
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Since P(x) is odd, let it be P(x) = ax^3 + bxp(x) is an odd polynomial of degree 3. It has x+4 as a factor, and when it is divided by x-3, the remainder is 21. Find p(x).
It has x+4 as a factor, so P(-4) = 0. (factor theorem)
It has remainder 21 when divided by x-3, so P(3) = 21 (remainder theorem)
You should have two expressions in terms of 'a' and 'b'.
Solve simultaneously.
mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
where is this equation from ax^3 + bxSince P(x) is odd, let it be P(x) = ax^3 + bx
It has x+4 as a factor, so P(-4) = 0. (factor theorem)
It has remainder 21 when divided by x-3, so P(3) = 21 (remainder theorem)
You should have two expressions in terms of 'a' and 'b'.
Solve simultaneously.
Velocifire
Critical Hit
- Joined
- Sep 7, 2019
- Messages
- 805
- Gender
- Undisclosed
- HSC
- 2021
2013 guys 
Because it says P(x) is an odd polynomial. With an odd function P(x) = -P(x).where is this equation from ax^3 + bx
It also has degree 3. You can only have a degree 3 polynomial of the form ax^3 + bx that is an odd function because
If you add in any of the other terms such as x^2 or x or the constant, you won't have an odd function. For example if you take P(x) = ax^3 + bx^2 +cx then you get
It's how you do these questions. You write out a general equation of P(x) where the values of a, b, c... and so forth being random numbers.
mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
ok i get this but the thing is where did you pull this equation fromBecause it says P(x) is an odd polynomial. With an odd function P(x) = -P(x).
It also has degree 3. You can only have a degree 3 polynomial of the form ax^3 + bx that is an odd function because
If you add in any of the other terms such as x^2 or x or the constant, you won't have an odd function. For example if you take P(x) = ax^3 + bx^2 +cx then you get
what is the formula for odd polynomial or even polynomial for degree 2, 4, 5 so on...
B1andB2
oui oui baguette
for a function, if f(-x)=-f(x), then the function is odd. If f(-x)=f(x), then it is evenok i get this but the thing is where did you pull this equation from
what is the formula for odd polynomial or even polynomial for degree 2, 4, 5 so on...
B1andB2
oui oui baguette
i remember this question from cambridge... tripped me up a lot lol
mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
This is exactly the part i don't getu can prove that necessarily that the polynomial is ax^3+cx
Let f(x) = ax^3+bx^2+cx+d, a third degree polynomial
Since f(x) is odd, f(-x)=-f(x), i.e. -ax^3+bx^2-cx+d=-ax^3-bx^2-cx-d
Thus bx^2+d=0
Thus f(x)=ax^3+cx
how do you go from
bx^2+d = 0
to
f(x) = ax^3+cx
bx^2+d doesn't equal to ax^3+cx does it not?
The equation initially is f(x) = ax^3 + bx^2 +cx + d. Which rearranged is f(x) = ax^3 + cx + (bx^2 + d).This is exactly the part i don't get
how do you go from
bx^2+d = 0
to
f(x) = ax^3+cx
bx^2+d doesn't equal to ax^3+cx does it not?
If you sub in bx^2 + d = 0 into that equation what remains is ax^3 + cx.
mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
thank you geniusThe equation initially is f(x) = ax^3 + bx^2 +cx + d. Which rearranged is f(x) = ax^3 + cx + (bx^2 + d).
If you sub in bx^2 + d = 0 into that equation what remains is ax^3 + cx.
Generalising, an even polynomial can only have terms with even powers and an odd polynomial can only have terms with odd powers. Further, if the degree of the polynomial is even then the polynomial cannot be odd but it can be even (though it could also be neither odd nor even). Similarly, if the degree of the polynomial is odd then the polynomial cannot be even but it can be odd (though it could also be neither odd nor even).
Taking = a_0 + a_1 + a_2x^2 + a_3x^3 + ... + a_{2n}x^{2n}) :
:
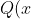 = a_0 + a_1 + a_2x^2 + a_3x^3 + ... + a_{2n+1}x^{2n+1}) :
:
) can be partitioned into two functions:
can be partitioned into two functions:
) and if
and if  = 0) then the function is odd, and if
then the function is odd, and if  = 0) then it is even. This partition is not useful for all functions. For example,
then it is even. This partition is not useful for all functions. For example,  = \sqrt{x}) is neither odd nor even and the partition does not yield a useful / sensible partition into an odd function and an even function. By contrast,
is neither odd nor even and the partition does not yield a useful / sensible partition into an odd function and an even function. By contrast, 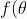 = \theta - \cos\theta + \sin\theta) is usefully separable into an odd component
is usefully separable into an odd component  = \theta + \sin\theta) and an even component
and an even component  = -\cos\theta) .
.
Applying this to the above problem, we need an odd function of degree 3. Starting from
 = ax^3 + bx^2 + cx + d)
we have
 &= \cfrac{1}{2}\Big[P(x) - P(-x)\Big] \\ &= \cfrac{1}{2}\Big[ax^3 + bx^2 + cx + d - \big(a(-x)^3 + b(-x)^2 + c(-x) + d)\big)\Big] \\ &= \cfrac{1}{2}\Big[ax^3 + bx^2 + cx + d - \big(-ax^3 + bx^2 - cx + d\big)\Big] \\ &= \cfrac{1}{2}\Big[ax^3 + bx^2 + cx + d + ax^3 - bx^2 + cx - d\Big] \\ &= \cfrac{1}{2}\Big[2ax^3 + 2cx\Big] \\ &= ax^3 + cx \end{align*})
and we need the even part to be zero, which is how the above solutions established that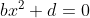 . This can be shown as follows:
. This can be shown as follows:
 = P_E(x) + P_O(x) \implies P_E(x) &= P(x) - P_O(x) \\ &= ax^3 + bx^2 + cx + d - \big(ax^3 + cx\big) \\ &= ax^3 + bx^2 + cx + d - ax^3 - cx \\ &= bx^2 + d \\ \text{And, since $P(x)$ is odd, $P_E(x) = 0$:} \qquad bx^2 + d &= 0 \end{align*})
Taking
is even if and only if
cannot be odd and a polynomial of degree
is odd if and only if
cannot be even and a polynomial of degree
, an even function, and
, an odd function, such that
. This can be achieved by defining:
Applying this to the above problem, we need an odd function of degree 3. Starting from
we have
and we need the even part to be zero, which is how the above solutions established that
Last edited:

