Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Polynomials!? (1 Viewer)
- Thread starter Currybear
- Start date
i tried and i got a strange equation with both x and y's so i used to quad formula
then i got a +- value which is tripppin me up
if possible could you do the question on paper and send me the photo, i know its a lot to ask but it would be much obliged
then i got a +- value which is tripppin me up
if possible could you do the question on paper and send me the photo, i know its a lot to ask but it would be much obliged
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Ok so you have
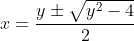 which when substituted becomes
which when substituted becomes
^3 + 3\left(\frac{y\pm \sqrt{y^2-4}}{2}\right) + 2=0 )
Now just consider the positive square root for now.
Multiply through by 8 to get rid of all denominators. Then use the binomial theorem to expand the first cubed bracket. Collect all the non-surd terms on one side and the surd terms on the other. Square both sides to get rid of the surd. Now simplify (lots of algebra). Do the same with the negative case (or just see where your negatives pop up and change accordingly).
Now just consider the positive square root for now.
Multiply through by 8 to get rid of all denominators. Then use the binomial theorem to expand the first cubed bracket. Collect all the non-surd terms on one side and the surd terms on the other. Square both sides to get rid of the surd. Now simplify (lots of algebra). Do the same with the negative case (or just see where your negatives pop up and change accordingly).
Think about it. Which specific terms have the 'minus' with them (as opposed to their positive counterparts)? What will happen to these later then you square both sides to get rid of the surd?
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
Begin with the usual transformation.
Let y=x+1/x. Now solve this equation for x and then substitute this expression (in terms of y) into your original equation and you're done.
asianese your method is not quite right i will tell you the right answer in approx 5 minutes
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
=x^3 + 3x + 2 = 0
has roots a, b, y
therefore
1. a + b + y = 0
2. ab + ay + by = 3
3. aby = -2
Now using these identities
For the new equation coefficient of x^2
is
-(a + b + y + 1/a + 1/b + 1/y)
using simple algebra
= 3/2
coefficient of X this part is just crazy long
= (a + 1/a)(b + 1/b) + (b + 1/b)(y +1/y) + (y + 1/y)(a + 1/a)
= ab + a/b + b/a +1/ba + ay + a/y + y/a +1/by + ay + a/y + y/a +1/ya
simplifying
= (ab + by + ay) +(a+y)/b + (b+a)/y + (y+b)/a + (a + b + y)/aby
note a + b + y = 0
hence a + b = -y
=3 + (-b/b) + (-y/y) +(-a/a) +0
= 3 - 1 - 1 -1
= 0
now i am quite exhausted typing i will post the second part of answer soon
has roots a, b, y
therefore
1. a + b + y = 0
2. ab + ay + by = 3
3. aby = -2
Now using these identities
For the new equation coefficient of x^2
is
-(a + b + y + 1/a + 1/b + 1/y)
using simple algebra
= 3/2
coefficient of X this part is just crazy long
= (a + 1/a)(b + 1/b) + (b + 1/b)(y +1/y) + (y + 1/y)(a + 1/a)
= ab + a/b + b/a +1/ba + ay + a/y + y/a +1/by + ay + a/y + y/a +1/ya
simplifying
= (ab + by + ay) +(a+y)/b + (b+a)/y + (y+b)/a + (a + b + y)/aby
note a + b + y = 0
hence a + b = -y
=3 + (-b/b) + (-y/y) +(-a/a) +0
= 3 - 1 - 1 -1
= 0
now i am quite exhausted typing i will post the second part of answer soon
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
Now
constant
= - (a+1/a)(b+1/b)(y+1/y)
= - (aby + ab/y + ay/b + by/a + a/by + b/ay + y/ab + 1/aby)
quite long X_X
= -(-2 + -1/2 + (a^2b^2 + ......)
now i give up typing
if you re doing 4 unit you should know what to do from this step onwards
keep simplifying and you get
4
hence equation is
2x^3 + 3x^2 + 8 = 0
constant
= - (a+1/a)(b+1/b)(y+1/y)
= - (aby + ab/y + ay/b + by/a + a/by + b/ay + y/ab + 1/aby)
quite long X_X
= -(-2 + -1/2 + (a^2b^2 + ......)
now i give up typing
if you re doing 4 unit you should know what to do from this step onwards
keep simplifying and you get
4
hence equation is
2x^3 + 3x^2 + 8 = 0
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
if there is another way of doing it please post
although i am pretty sure that this is the best and fastest method.
Trust me you will NEVER NEVER get this question in any test
Reason
:1. too fu***** long
2. at least 3 pages of working
If it does come out, i will kill myself unless the question is like 10 mark
although i am pretty sure that this is the best and fastest method.
Trust me you will NEVER NEVER get this question in any test
Reason
:1. too fu***** long
2. at least 3 pages of working
If it does come out, i will kill myself unless the question is like 10 mark
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
true asianese this question is just a joke
cineti970128
Member
- Joined
- Apr 25, 2012
- Messages
- 139
- Gender
- Male
- HSC
- 2014
My bad i didnt read that also the fact that the positive and negative sign does get lostYes. You can use the sum of roots and sum of reciprocal of roots to form a new equation. In hindsight this is easier.
sorry X_X
Do you think this kind of question will come out in any exams?
hayabusaboston
Well-Known Member
Begin with the usual transformation.
Let y=x+1/x. Now solve this equation for x and then substitute this expression (in terms of y) into your original equation and you're done.
Perfect word hahaha :')
hayabusaboston
Well-Known Member
I had it in my exam boi.My bad i didnt read that also the fact that the positive and negative sign does get lost
sorry X_X
Do you think this kind of question will come out in any exams?
Speaking of which, rank 1 in half yearly ext 1 maths FUCK YEA


