Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Here are two not-so-difficult problems I thought of a few days ago. It should be do-able for a keen 3U student.
Problem #1:

Consider the following *poorly drawn* diagram. We start with a right angled triangle of hypotenuse length n. The 'base' of this triangle is the hypotenuse of another triangle, and so the process repeats until it can no longer continue. The length of the other side is kept as a constant 1.
Define the sum of k triangles to be S(k), such that

Show that:
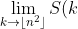 < \frac{1}{3}n^{3} )
Problem #2:

A man starts at point X. He walks 1m North. He then walks 2m East, then 3m South, then 4m West etc etc until he finally walks N metres either N/S/E/W, depending on N.
Find the distance the man is from the X after the 'lap' involving him walking N metres.
Interesting variation to Problem #2:
A man starts from some point X. He walks 1m North. He then walks 1/2m East, then 1/3m South, then 1/4m West etc and continues with this pattern indefinitely.
Will he reach a finite point? If so, how far is it from his original position X? <a< \sqrt="" n="" \frac{2n+3}{3}[="" tex]<="" html=""></a<>
Problem #1:

Consider the following *poorly drawn* diagram. We start with a right angled triangle of hypotenuse length n. The 'base' of this triangle is the hypotenuse of another triangle, and so the process repeats until it can no longer continue. The length of the other side is kept as a constant 1.
Define the sum of k triangles to be S(k), such that
Show that:
Problem #2:

A man starts at point X. He walks 1m North. He then walks 2m East, then 3m South, then 4m West etc etc until he finally walks N metres either N/S/E/W, depending on N.
Find the distance the man is from the X after the 'lap' involving him walking N metres.
Interesting variation to Problem #2:
A man starts from some point X. He walks 1m North. He then walks 1/2m East, then 1/3m South, then 1/4m West etc and continues with this pattern indefinitely.
Will he reach a finite point? If so, how far is it from his original position X? <a< \sqrt="" n="" \frac{2n+3}{3}[="" tex]<="" html=""></a<>
Last edited:

