Pythagorean Triads (1 Viewer)

[seanieg89]

We define a primitive Pythagorean triad to be a triple of positive integers (a,b,c) with greatest common divisor 1 such that:



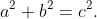
Examples of Pythagorean triads include (3,4,5) and (5,12,13).

In this question we find ALL primitive Pythagorean triads using high-school level methods.

Let Q denote the open first quadrant of the unit circle. (ie .)

i) Prove that there is a one-to-one correspondence between the primitive Pythagorean triads and the points on Q with rational coordinates.

ii) Let denote the line through with gradient . Prove that meets 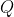at a point with rational coordinates if and only if 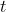is rational.

iii) Using the previous parts and the fact that a positive rational number can be written UNIQUELY in reduced form, find a parametric formula that gives every primitive Pythagorean triad.</t<1[></t<1[>

 

[seanieg89]

Anyone want to have a crack at it? It isn't beyond an interested MX2 student. I will post a solution tomorrow otherwise.

 

[Carrotsticks]

This is what I got:

The line l_t has the general equation:

y = t (x+1)

For some t E (0,1)

The equation of the unit circle is:



Solving these two simultaneously and making it into a quadratic yields:



Sum of roots is:



Where X is the point where the line intersects the circle and -1 is the fixed point previously mentioned.

Solving for x yields the equivalent t formula for cos(theta):



Let t = p/q for relatively prime integers p and q.



And this is rational if and only if t is also rational.

Subbing back into the equation of the line or circle yields the t formula for sin(theta):



Which is rational iff t is rational.

So our parametric expression for the triads are:



For some integers p and q such that q > p.

For any t E (0,1), we have x^2 + y^2 = 1:

So suppose we pick t = 0.5:



Which is indeed the trivial Pythagorean Triad.

Not quite sure how to prove the one-to-one correspondence.

This proof is essentially using the ~sorta~ stereographic projection of the unit circle. I emphasise the 'sorta' because in a sense it is kinda the reverse, and we are taking the projection sideways as opposed to downwards.

 

[Carrotsticks]

Actually, just realised with the x coordinate, t could be something like 1/sqrt(2), which would still yield a rational number.

Have to revise my answer.

 

[barbernator]

<a href="http://www.codecogs.com/eqnedit.php?latex=let~t=m\\ y=mx@plus;b\\ line~passes~through~point~(-1,0)\\ m=b\\ y=m(1@plus;x)\\ sub~into~equation~of~circle\\ x^2@plus;m^2(1@plus;x)^2=1\\ making~x~the~subject\\ x^2@plus;m^2x^2@plus;2m^2x=1-m^2\\ x^2@plus;\frac{2m^2}{1@plus;m^2}x=\frac{1-m^2}{1@plus;m^2}\\ completing~the~square\\ (x@plus;\frac{m^2}{1@plus;m^2})^2=\frac{1}{(1@plus;m^2)^2}\\ x=\pm\sqrt{\frac{1}{(1@plus;m^2)^2}}-\frac{m^2}{1@plus;m^2}\\ x=\frac{1-m^2}{1@plus;m^2}\\ substituting~m=\frac{1}{\sqrt{2}}~x=\frac{1}{3}~what?!!! just~realised~i~took~a~long~way~around~but~eh" target="_blank"><img src="http://latex.codecogs.com/gif.latex?let~t=m\\ y=mx+b\\ line~passes~through~point~(-1,0)\\ m=b\\ y=m(1+x)\\ sub~into~equation~of~circle\\ x^2+m^2(1+x)^2=1\\ making~x~the~subject\\ x^2+m^2x^2+2m^2x=1-m^2\\ x^2+\frac{2m^2}{1+m^2}x=\frac{1-m^2}{1+m^2}\\ completing~the~square\\ (x+\frac{m^2}{1+m^2})^2=\frac{1}{(1+m^2)^2}\\ x=\pm\sqrt{\frac{1}{(1+m^2)^2}}-\frac{m^2}{1+m^2}\\ x=\frac{1-m^2}{1+m^2}\\ substituting~m=\frac{1}{\sqrt{2}}~x=\frac{1}{3}~what?!!! just~realised~i~took~a~long~way~around~but~eh" title="let~t=m\\ y=mx+b\\ line~passes~through~point~(-1,0)\\ m=b\\ y=m(1+x)\\ sub~into~equation~of~circle\\ x^2+m^2(1+x)^2=1\\ making~x~the~subject\\ x^2+m^2x^2+2m^2x=1-m^2\\ x^2+\frac{2m^2}{1+m^2}x=\frac{1-m^2}{1+m^2}\\ completing~the~square\\ (x+\frac{m^2}{1+m^2})^2=\frac{1}{(1+m^2)^2}\\ x=\pm\sqrt{\frac{1}{(1+m^2)^2}}-\frac{m^2}{1+m^2}\\ x=\frac{1-m^2}{1+m^2}\\ substituting~m=\frac{1}{\sqrt{2}}~x=\frac{1}{3}~just~realised~i~took~a~long~way~around~but~eh" /></a>

 

[seanieg89]

For ii) I should clarify something. A point having rational coordinates means BOTH of its coordinates are rational. This is NOT equivalent to having a rational x-coordinate.