-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Quick Math Question Help! (1 Viewer)
- Thread starter SGSII
- Start date
espiritulol
Member
espiritulol
Member
Sorry I don't think I can get the other one
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
For Question 10.
Think about how you would curl the sector into a cone, you will notice that the arc length of the sector, is the circumference of the base circle of the cone.
Surface Area will be the area of the sector, I don't think it will include the inside surface, but if it is, multiply result by 2.
So for Surface Area,

To find Volume of the cone:

To find the radius of the cone, we need to find the radius of the circle formed at the bottom. To do this, we will use what we know, which is the circumference of said circle.
We know that the circumference is
Now we know that:

So we know C the circumference, lets find the radius.


Now last thing we need to know is the height of our cone, again imagining curling our sector.
To imagine what the height is, first draw a line connecting the two ends of the sector which are joining the curved edge, so we now have a triangle. The height of the cone is the perpendicular from the centre of the sector to that line we made earlier. To find the length of the line, simple trigonometry is applied.


We use pi/6 since we split the angle in half when applying our right angle trig (I advise you to draw all these steps out to make it clearer).
Now we have height and radius, we can find our Volume to be.
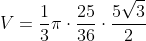
Think about how you would curl the sector into a cone, you will notice that the arc length of the sector, is the circumference of the base circle of the cone.
Surface Area will be the area of the sector, I don't think it will include the inside surface, but if it is, multiply result by 2.
So for Surface Area,
To find Volume of the cone:
To find the radius of the cone, we need to find the radius of the circle formed at the bottom. To do this, we will use what we know, which is the circumference of said circle.
We know that the circumference is
Now we know that:
So we know C the circumference, lets find the radius.
Now last thing we need to know is the height of our cone, again imagining curling our sector.
To imagine what the height is, first draw a line connecting the two ends of the sector which are joining the curved edge, so we now have a triangle. The height of the cone is the perpendicular from the centre of the sector to that line we made earlier. To find the length of the line, simple trigonometry is applied.
We use pi/6 since we split the angle in half when applying our right angle trig (I advise you to draw all these steps out to make it clearer).
Now we have height and radius, we can find our Volume to be.



