asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
The hyperbola  touches the circle
touches the circle ^2+y^2=1) at the point Q.
at the point Q.
i) Show this information on a sketch.
ii) Show that if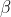 is a repeated root of the polynomial equation
is a repeated root of the polynomial equation =0) then
then 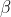 is also a root of
is also a root of 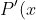=0)
iii) Deduce that the equation^2+c^4=x^2) has a repeated root
has a repeated root  , and two non-real complex roots.
, and two non-real complex roots.
iv) Find the values and the remaining roots of the equation
and the remaining roots of the equation ^2+c^4=x^2)
v) Find the equation of the common tangent to the hyperbola and the circle at Q.
I'm having trouble with iii)...Do I sub in c^4? I get it equalling 0 which is not good. Any tips/hints would be very much appreciated.
Thankyou!
i) Show this information on a sketch.
ii) Show that if
iii) Deduce that the equation
iv) Find the values
v) Find the equation of the common tangent to the hyperbola and the circle at Q.
I'm having trouble with iii)...Do I sub in c^4? I get it equalling 0 which is not good. Any tips/hints would be very much appreciated.
Thankyou!
Last edited:


