Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,145
- Gender
- Male
- HSC
- 2010
So I'm doing some power solutions to DEs and I get expressions like this:
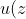 = A_{0} \left ( 1 - \frac{1}{2}z^{2} + \frac{1}{8}z^{4} - \frac{1}{48}z^{6} + ... \right ) + A_{1} \left (z - \frac{1}{3}z^{3} + \frac{1}{15}z^{5} - \frac{1}{105}z^{7} + ... \right ))
with
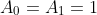
given.
And the solution at the 'back of the book' is:
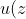 = \sum_{k=0}^{\infty} \frac{\left (z^{2}/2 \right )^{k}}{k!} + z \sum_{k=0}^{\infty} \frac{k!}{(2k+1)!}(-2z^{2})^{k})
And if we compare, we see that the two solutions match up (well, at least appear to do so after four terms)
My question is: How do I go from my power series above - to the neat summation at the bottom?
Is there a trick? Or is the solution provided just a quick way to summarise the series and I'm not actually required to do such a thing, because my expansion is equivalent anyway...
any and all help is appreciated
thanks in advance!
edit:
not sure if this is relevant, but the recurrence used to achieve the expansion is
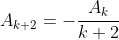
for k = 0, 1, 2, ...
with
given.
And the solution at the 'back of the book' is:
And if we compare, we see that the two solutions match up (well, at least appear to do so after four terms)
My question is: How do I go from my power series above - to the neat summation at the bottom?
Is there a trick? Or is the solution provided just a quick way to summarise the series and I'm not actually required to do such a thing, because my expansion is equivalent anyway...
any and all help is appreciated
thanks in advance!
edit:
not sure if this is relevant, but the recurrence used to achieve the expansion is
for k = 0, 1, 2, ...
Last edited:

