Fair enough, it is pretty much just application of the definitions:
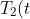=x'(t)=B_1(t))
and hence x moves at unit speed in the direction of the Binormal vector of r at time t.
To compute the curvature of x, as usual we differentiate T.
So
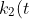N_2(t)=T_2'(t)=B_1'(t)=-t_1(t)N_1(t))
where
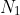
, and
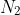
have unit length, and the first and last equalities follow from the definition of curvature and torsion respectively.
Hence
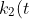=|k_2(t)|=|-t_1(t)|=|t_1(t)|)
(recall that curvature of a curve is a positive quantity).
This also implies that
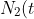=-N_1(t))
by normalisation.
Now that we know the tangent and normal vectors of x, we can compute its binormal.
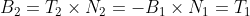
(the last equality can be justified in multiple ways, eg Jacobi's identity for the cross product or by noting that it is clearly a multiple of
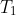
since it is orthogonal to both
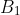
and
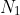
, and also that it has length one since
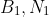
are unit length and orthogonal. Then it is just a matter of checking signs.)
Hence
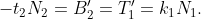
Since we have already established
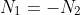
, this implies
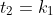
.
This completes the calculation.
