1. Solve the equation 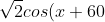-1=0 for 0\leq x\leq 360)
2. P (2ap, ap^2) and Q (2aq, aq^2) are 2 points on the parabola x^2= 4ay with parameter values p=4 and q=-6. Show that the lines OP and OQ are inclined at 45 degrees to each other.
3. Solve the inequality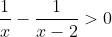
4. Show that 2cos(A - B)sin(A+B)= sin2A + sin 2B
5. The polynomial eq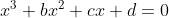 has roots
has roots
a, a^2 and a^3
Find in terms of b,c and d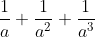
Show that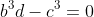
thanks.
2. P (2ap, ap^2) and Q (2aq, aq^2) are 2 points on the parabola x^2= 4ay with parameter values p=4 and q=-6. Show that the lines OP and OQ are inclined at 45 degrees to each other.
3. Solve the inequality
4. Show that 2cos(A - B)sin(A+B)= sin2A + sin 2B
5. The polynomial eq
a, a^2 and a^3
Find in terms of b,c and d
Show that
thanks.
