asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Want to get these out before sleepin:
Find the limit, or show it doesn't exist:
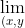\to(0,0)} \dfrac{x^3+y^3}{x^2-y^2})
The usual tricks like factorising/cancelling, going polar, x=y, x=0, y=0 don't seem to work? Probs blanking out. I know it doesn't exist but I can't find a path which isn't 0.
Next:


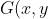 = \left\{\begin{array}{lr} \dfrac{f(y)-f(x)}{y-x} & : y\ne x\\ f'(x) & : y=x\end{array}\right.)
. $ Hint: the recommended method is to replace $ f(y) $ by its Taylor polynomial $T_3(y)$ about $y=x. $ Methods based on l'Hopital's rule or the chain rule for partial derivatives will also work.$)
I get the partial deriv is f'(x) but i definitely did something wrong
Find the limit, or show it doesn't exist:
The usual tricks like factorising/cancelling, going polar, x=y, x=0, y=0 don't seem to work? Probs blanking out. I know it doesn't exist but I can't find a path which isn't 0.
Next:
I get the partial deriv is f'(x) but i definitely did something wrong
Last edited:

