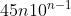Sum of digits. (1 Viewer)

[Fus Ro Dah]

 

[johnpap]

Just doing it recursively, if Tn is what you want T1=45 by observation, then
T(n+1) = Tn + (Sum of digits of n+1 digit numbers) = Tn + 9Tn (Training n digits of n+1 digit numbers) + 45*10^(n-1) (Leading digits cycle and occur 10^n-1 times each)

So Tn = (45*n)*10^(n-1) if I didn't mess up solving the recurrence. E.g. the series goes 45, 900, 13500, 180 000 ...

 

[RealiseNothing]

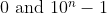
Consider you wrote down every possible number between going down the page directly underneath each other. Do in such a way that they all contain equal amounts of digits. i.e. if you were to write the numbers from 0 to 99, you would write 0 as 00, 1 as 01, etc, since 99 has two digits, and hence we want every number we write to have 2 digits.

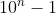
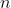
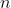
has digits, so we can write the numbers all with digits as so:











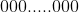
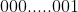
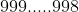
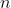
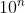
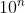
This forms a rectangle with length digits, and height digits since there are numbers between

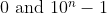
Hence the total amount of digits present is

Since all digits occur an equal amount of times (you can replace any number with a different number and it wouldn't change the amount of permutations), it follows that each digit occurs times.

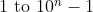
Hence the sum of all the digits from is:



Which simplifies to give our answer of:

 

[Fus Ro Dah]

Both correct^^. RealiseNothing, your solution is very intuitive.