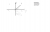Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
In the preliminary version, its called ASTC, (All Sine Tan Cos)
Here is a crappy diagram
The logic behind ASTC is from trigonometric graphs, when you graph y=sin(x), between 270 and 360 degrees (3pi/2 and 2pi) the curve of y=sinx is below the x-axis, therefore it is negative, and since the graph is symmetrical, you get the exact answer.

In this diagram, the higlighted part, is where Sin is negative.
And the logic behind sin(90-x) = cosx
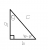
Take a normal right angle triangle, one angle is theta, the other is 90 - theta (angle sum of triangle)
In here I put x as theta, because Im adumb with latex
According to the triangle:
sin(x) = b/a
but if you take the cosine of the OTHER angle
cos(90-x) = b/a
Therefore:
cos(90-x)=sin(x)
and vice versa
Here is a crappy diagram
The logic behind ASTC is from trigonometric graphs, when you graph y=sin(x), between 270 and 360 degrees (3pi/2 and 2pi) the curve of y=sinx is below the x-axis, therefore it is negative, and since the graph is symmetrical, you get the exact answer.

In this diagram, the higlighted part, is where Sin is negative.
And the logic behind sin(90-x) = cosx

Take a normal right angle triangle, one angle is theta, the other is 90 - theta (angle sum of triangle)
In here I put x as theta, because Im adumb with latex
According to the triangle:
sin(x) = b/a
but if you take the cosine of the OTHER angle
cos(90-x) = b/a
Therefore:
cos(90-x)=sin(x)
and vice versa
Last edited: