Part ii/iii written out:
In part i you would find:
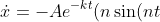+k\cos(nt)))
To find when particle is rest set
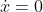
which you would do in part ii
+k\cos(nt))=0)
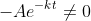
so solve:
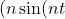+k\cos(nt))=0)
mucking around with auxiliary angle (or you could just divide by cos) we get:
=0 \hspace{3mm}\text{where}\hspace{3mm} \alpha=\arctan(\frac{k}{n}))
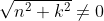
so solve:
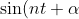=0)
not sure if general solutions is in the syllabus so I'll just list out the solutions
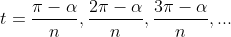
Then sub this into x (keeping in mind the displacement will be negative) you will get the answer for ii.
For part iii like previous posters said take the infinite sum so we get the sum (i'll write it out long assuming general sol isn't in the syllabus):
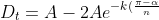}\cos(\pi-\alpha)+2Ae^{-k(\frac{2\pi-\alpha}{n})}\cos(2\pi-\alpha)-2Ae^{-k(\frac{3\pi-\alpha}{n})}\cos(3\pi-\alpha)+...)
Notice the pattern for odd multiples of
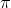
cosine is negative and for even multiples of
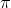
it's positive. So simplifying the sum:
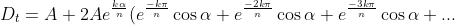)
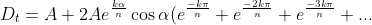)
We can see the sum is convergent quite easily but a formal proof is prob required. Using the GP sum we finally get:
)
)
) \hspace{3mm} \text{drawing up a triangle we find} \hspace{3mm} \cos({\arctan(\frac{k}{n}))=\frac{n}{\sqrt{n^2+k^2})


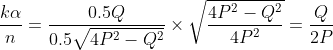
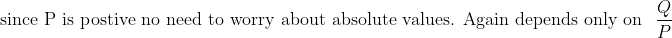
.
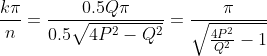
Therefore every part of the expression for
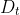
depends solely on the fraction
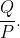
(notice that A is constant so we don't have to worry about that).
Sidenote: Sorry for the terrible latex

. I also probably included too many steps which wouldn't be required in a typical exam.

