Could someone please check if my answer is correct?
A tank with plane sides has square horizontal cross-sections whose sides cary in length from 2 m at the base to 5 m at the top; the height is 12 m. Find the total mass of liquid in the tank, if the density decreases uniformly with the height from 20kg/m^3 at the bottom to 12kg/m^3 at the top
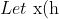=ah+b $ be the side length of the square cross section at heigh $ h $. When h=0, x=2. When h=12, x=5 $\Rightarrow x=\frac{1}{4}h+2 \\ \\ \therefore \delta V= (\frac{1}{4}h+2)^2 \delta h \\ \Rightarrow V=\int_{0}^{12}\left ( \frac{1}{4}h+2 \right )^2 $ d$h = 156$ m$^3 \\ \\ \frac{\mathrm{d} \rho}{\mathrm{d} h} = -k \Rightarrow \rho = -hk+c$ When $h=0, \rho=20. $ When $h=12, \rho =12 \\ \Rightarrow \rho=-\frac{2}{3}h+20. \\ \\\therefore $ Density of the whole solid $=\int_{0}^{12}\left ( -\frac{2}{3}h+20 \right )$ d$h = 192$ kgm$^{-3} \\ \\ \rho = \frac{m}{v} \Rightarrow m = \rho v = 192\cdot 156 = 29952 $ kg$ )
A tank with plane sides has square horizontal cross-sections whose sides cary in length from 2 m at the base to 5 m at the top; the height is 12 m. Find the total mass of liquid in the tank, if the density decreases uniformly with the height from 20kg/m^3 at the bottom to 12kg/m^3 at the top
