Volumes past paper Q (1 Viewer)
- Thread starter K4M1N3
- Start date
hscishard
Active Member
Try the addition of the vertical ellipse solid and the solid rotated by the straight line, with the bounds x=3-5 or y=0-5, however your approach is (slices or shells)
Curious on where you got thequestion from
Curious on where you got thequestion from
What is this object like? is the elliptical base 10 metres long and 4 metres wide? I thought a pier is something flat ans long that stretches out to sea. Is it like a bath soap truncated across the middle and a little further along?? This object is like quite thick (5 m high) and only 10 m long at the base?
Is volume around 15.42 pi cubic metres ??
Which past paper is this from?
Edit(16 July 2011)

Is volume around 15.42 pi cubic metres ??
Which past paper is this from?
Edit(16 July 2011)
Last edited:
hscishard
Active Member
^ I know right, the pier part was odd so I just ignored it and drew a diagram. I ended up with a solid that has a 2D trapezium side view
K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
OMG im so glad others cant visual the shape either...i was shitting myself :S..
Yeah i know the pier your thinking of drongoski, but i dont think this is the same thing, I think it looks like a beaker of sorts, just with an elliptical base and an elliptical opening. However the object is vertically symmetrical from one horizontal view (front) it is not from the other (side).
This was from the 2000 JR trial.
Yeah i know the pier your thinking of drongoski, but i dont think this is the same thing, I think it looks like a beaker of sorts, just with an elliptical base and an elliptical opening. However the object is vertically symmetrical from one horizontal view (front) it is not from the other (side).
This was from the 2000 JR trial.
Last edited:
hscishard
Active Member
hscishard
Active Member
Yea...like a deformed cork
If so, the method I posted should work. I can't really explain it better and I haven't actually done the question lol
If so, the method I posted should work. I can't really explain it better and I haven't actually done the question lol
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
I solved it using co-ordinate geometry. you let the cross-section have height delta x. then using co-ordinate geometry find an expression for the semi-major axis of the cross-section in terms of x. also do this for the semi-minor axis. then using limits 0 to 5, solve integral in terms of x to get and answer of:
185pi/6
185pi/6
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
i meant thickness of sliceWhen you say height being dx, do you rly mean height, or thickness of slice? Because the height would be changing since its the value of a or b (depending on visual orientation).
hscishard
Active Member
arj1 method is a good way I guess. Strange how I didn't think of that first...
K4M1N3
Member
- Joined
- Jun 7, 2010
- Messages
- 177
- Gender
- Male
- HSC
- 2011
How did you derive the relationship between "z" and a and b?
Also i did an approximation imagining a whole elliptical cone. The approximation was (50pi)/3 ~ 52.3..... Which is just over your answer of 185pi/12 drongoski, so im going to assume you made correct calculations.
Also i did an approximation imagining a whole elliptical cone. The approximation was (50pi)/3 ~ 52.3..... Which is just over your answer of 185pi/12 drongoski, so im going to assume you made correct calculations.
Last edited:
I could have used x instead of z. Here I'm thinking in terms of the x, y and z axes in 3-D space (but this is not really necessary). So I used the z-axis where in 2-D you'd normally use the y-axis. Unfortunately I don't know how to put up a hand-written solution with diagrams; else explaining would be much easier.
Any value of z (0 <= z <= 5) determines an ellipse parallel to the base ellipse; the 'a' and 'b' of this ellipse is found by considering the cross-section thru the z-axis one parallel to the x-axis and the other, the y-axis.
In each case, join the left extremity of the base ellipse to the "left" extremity of the top ellipse; this line has equation z = 5x/2 + D. z=0 when x = -3 ==> D = 25/2. .: this line has eqn: z = 5x/2 + 26/2 ==> x = (2z-25)/5
Similarly we find that the other slope has eqn: z = 5y + 10 ==> y = (z-10)/5
At any height z: the corresponding ellipse has "a" and "b" given by:


Therefore this ellipse has area: = \pi a b = \pi \times (\frac {25-z}{5})(\frac {10-z}{5}) = \frac {\pi}{25} (250 - 45z + 2z^2))
 \delta z )
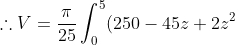 dz = \frac {185 \pi}{6} m^3 )
Any value of z (0 <= z <= 5) determines an ellipse parallel to the base ellipse; the 'a' and 'b' of this ellipse is found by considering the cross-section thru the z-axis one parallel to the x-axis and the other, the y-axis.
In each case, join the left extremity of the base ellipse to the "left" extremity of the top ellipse; this line has equation z = 5x/2 + D. z=0 when x = -3 ==> D = 25/2. .: this line has eqn: z = 5x/2 + 26/2 ==> x = (2z-25)/5
Similarly we find that the other slope has eqn: z = 5y + 10 ==> y = (z-10)/5
At any height z: the corresponding ellipse has "a" and "b" given by:
Therefore this ellipse has area:
Last edited:
Could then use double or triple integrals to find the volumeI could have used x instead of z. Here I'm thinking in terms of the x, y and z axes in 3-D space (but this is not really necessary).


