jet
Banned
- Joined
- Jan 4, 2007
- Messages
- 3,148
- Gender
- Male
- HSC
- 2009
OK, now that 2010 is here I am reviving the old Revision Marathon game.
Rules:
The OP posts a question, first person to get it correct asks the next question, and so on.
Full working MUST be shown before the answer is deemed correct.
Please try to write your solutions in LaTeX. If you can't, I will write it in LaTeX for you after you have posted it.
First Question
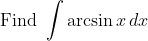
For those of you out of the loop,
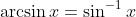
Rules:
The OP posts a question, first person to get it correct asks the next question, and so on.
Full working MUST be shown before the answer is deemed correct.
Please try to write your solutions in LaTeX. If you can't, I will write it in LaTeX for you after you have posted it.
First Question
For those of you out of the loop,
Last edited:
