Sketching the gradient function
Sketching the gradient function
So, I will quickly run you through the theory.
To fully understand how to sketch graphs of f prime x, we need to understand what we are actually doing when we are finding the gradient function. So let us begin this investigation!
We know the gradient function is a method we use to measure the gradient of the tangent at a particular
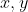
coordinate. So we will now utilised this powerful tool and sketch
A POSSIBLE curve for f prime x.
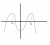
We will consider the following example. Over here we have a curve of
)
. Nasty examiners will not tell you the equation of this curve, so we can't directly fully use the beautiful art of Calculus to sketch the gradient function. But however, there is enough information to sketch a possible shape.

Our first reaction is we notice there is one minimum turning point and one maximum turning point. What would happen if I take a tangent at the corresponding

coordinate?

The tangents at those points are in fact horizontal. What does that mean? It means they have a gradient of zip! Zero!

How do we use this fact? On our original graph our axes were
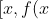])
. On our new graph our axes are now
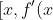])
When we take the derivative of a function and graph it , our

coordinate must stay the same. However our
)
oordinate changes. In this case, the minimum and maximum points will become

intercepts, since for maximum and minimum points (Stationary points),
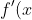=0)
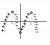
So we can now swipe them down onto our pretty
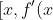])
coordinates. Like so. (Note: The read resembles the graph on the
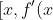])
(Just imagine it!) Sorry I had to do it on the same diagram for illustration.

Our graph is now divided into three regions! We must now consider each one. I will name the regions. A, B, C.

First letter of the alphabet goes first,
Region A.

Over in this region our gradient is always positive except at the top, we established that it was zero, so I will put little '+' s to indicate that, if you don't believe me, we will investigate this further by drawing tangents.
We're still in
Region A.

I have rated "arbitrary numbers" for the gradients to rate their steepness to illustrate my point. Clearly from Left to Right, our gradients are decreases. This means on our graph of from Left to Right
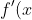)
values will decrease. In other words, our y coordinates will be decreasing as we go from Left to Right.
Or we can say as we go from Right to Left in that region, our y coordinates will tend towards infinity. So drawing our
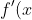)
graph in this region, we have something that looks like this.

Second, we will consider
Region B
Again for this region we notice the gradient is always negative. Let's arbitrarily rate the gradients again!

Remember these numbers are arbitrary!

This section we actually notice something very interesting, the gradients sort of get smaller, so the y coordinates of the graph f'(x) get smaller, but after that we hit a black spot. This spot is known as the point of inflexion. Then afterwards, we sort of rise back up again, and our gradients (y coordinates of f'(x) are getting larger.)
At the inflexion, our f'(x) graph will have a stationary point (minimum!) on the same x coordinates, but not necessarily the same y coordinates.
The inflexion is the lowest y coordinate of f'(x) we can get by inspecting the gradients! So this confirms it is a minimum!
So drawing this would look like.

Lastly,
Region C
We can obviously see throughout this region there are all positive gradients, so the graph will ALWAYS be above the x axis in this region.

Now, examining their gradient with arbitrary values!

Ah, as we go from Left to Right, the gradient is increasing, therefore our y coordinates of f'(x) are increasing too.
Finally your graph is now ready to be served and eaten!
 RAWWWWRR
RAWWWWRR
[
Editing]
-Refining detail and adding more description.