juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
No, the integral is clearly convergent in the interval [0,1] by the Comparison test, not to mention the fact that it has no singularities.Hmm, is this an improper integral by any chance?
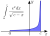
No, there is no asymptote at x=0. The function is well defined there, and is equal to 1.Lol, I have no idea what that means at all, I just remember reading a Wikipedia article about a month ago on this
http://en.wikipedia.org/wiki/Improper_integral
And since its an asymptote at 0. And it is an integral from 1 to 0 then I thought it was an Improper Integral.
View attachment 25438
i.e. ^^^ asymptote at c
Can't do that because the numerator is a separate function class from the denominator.Break the denominator up into a difference of two squares, then use partial fractions perhaps?
typed in wolfram, says its not integrate-able.fucking hell
wolframalpha.com
type it in, use brackets around the numerator and inside the sqrt sign and denominator. p much just bracket everything
everyone stop spamming BoS with integration q's when you can just type it in wolfram. you don't even need to know syntax just type in 'integrate xyz' and bam
jesus christ
Oh dear I've provided a reason against this so many times beforehand...fucking hell
wolframalpha.com
type it in, use brackets around the numerator and inside the sqrt sign and denominator. p much just bracket everything
everyone stop spamming BoS with integration q's when you can just type it in wolfram. you don't even need to know syntax just type in 'integrate xyz' and bam
jesus christ
http://www.wolframalpha.com/input/?i=\int_{0}^{1}\frac{\sqrt{1-x^2}}{1-x^2.\sin^2\%3Bx}dxtyped in wolfram, says its not integrate-able.

