RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
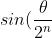 \to sin(0) = 0)
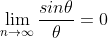
Do you mean like that?
As n approaches infinity,Find the other expression for it using part i (just divide by theta then take n to infinity)
Do you mean like that?

