HSC 2014 MX2 Marathon (archive) (5 Viewers)

dunjaaa · May 16, 2014

Re: HSC 2014 4U Marathon

What I was trying to do was inspect the stationary points, there probably is another way of proving this but it was the best I could do

Sy123 · May 17, 2014

Re: HSC 2014 4U Marathon

The way I did the upper bound was:

$f(x) = 1 - \frac{x^2}{\pi^2} - \cos x \ \Rightarrow \ f'(x) = - \frac{2x}{\pi} + \sin x$

$\\ $Since the function$ \ g(x) = \sin x \ $is concave, then the straight line through$ \ (0, g(0)), \left(\frac{\pi}{2} , g\left(\frac{\pi}{2} \right) \right) \ L \ $is so that$ \\ \\ \sin x \geq L \\ \\ L: \ \frac{2}{\pi} x \\ \\ \therefore \ \sin x - \frac{2}{\pi}x \geq 0 \ \Rightarrow \ f'(x) \geq 0 \\ \therefore \ f(x) \geq f(0) = 0 \\ \\ \therefore \ 1 - \frac{x^2}{\pi^2} \geq \cos x$

Davo_01 · May 17, 2014

Re: HSC 2014 4U Marathon

$\\$A projectile is launched at the edge of a house,which has a roof slanted at an angle of$\; 45^{\circ}.$The projectile just touches the roof (on both the left and right side of the house) when fired at a speed$\; V$and at an angle$\; \theta\; $.The walls of the house are h meters tall and the width of the house is equivalent to the range of the projectile,while the house is symmetrically shaped.$$

$\\$Show that the difference(L) in heights of the house and the maximum height of the projectile is given by:$\\ \\ L=\dfrac{d}{4} \\ \\$Where d is the distance between the two points of contact with the roof.$$

dunjaaa · May 21, 2014

Re: HSC 2014 4U Marathon

Can you provide us with a diagram, because I can't translate your instructions into one lol (idk if we have different interpretations of the way a house looks like)

dunjaaa · May 21, 2014

Re: HSC 2014 4U Marathon

Find the volume of the region bounded by the curve y=sin(x) between x=0 and x=pi rotated about the line y=-x.
If anyone else has any good oblique rotation questions, please share! It's in my upcoming assessment task even though its not in the syllabus and there isn't many questions I can source out from past papers or textbooks.

Ikki · May 22, 2014

Re: HSC 2014 4U Marathon

PHP:

dunjaaa said:
Can you provide us with a diagram, because I can't translate your instructions into one lol (idk if we have different interpretations of the way a house looks like)

I know right? Basically inside the house which apparently has nothing in it. At one end of the house it is fired and hits one side of the triangular shaped roof and then reaches its maximum and hits the other side and then falls to finish at the other side of the house. That is why the range is the length of the house.

Davo_01 · May 23, 2014

Re: HSC 2014 4U Marathon

dunjaaa said:
Can you provide us with a diagram, because I can't translate your instructions into one lol (idk if we have different interpretations of the way a house looks like)

Here you go, sorry if wording isn't clear enough

Davo_01 · May 23, 2014

Re: HSC 2014 4U Marathon

Ikki said:
PHP:

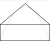
I know right? Basically inside the house which apparently has nothing in it. At one end of the house it is fired and hits one side of the triangular shaped roof and then reaches its maximum and hits the other side and then falls to finish at the other side of the house. That is why the range is the length of the house.

Well maybe its a dog house

Sy123 · May 25, 2014

Re: HSC 2014 4U Marathon

$\\ $For non-zero$ \ A,B,C \ $and$ \ A+B = C \ $if$ \ Ae^{ax} + Be^{bx} = Ce^{cx} \ \ (*) \ \ \ $for all$ \ x \\ \\ $i) Prove that$ \ a=b=c \ $is necessarily true$ \\ \\ $ii) If we drop the condition$ \ A+B = C \ $is there any$ \ a,b,c \ $so that the identity (*) holds true?$$

Not sure if it belongs in Advanced thread, I thought it was a bit easy to post there

Ikki · May 25, 2014

Re: HSC 2014 4U Marathon

i) From the condition given, A+B=C.
Multiply everything by e^x. Ae^x+Be^x=Ce^x.
Now the only way to reach the * form is to multiply throughout by the same constant which in this case means that a=b=c must hold true.

ii) As a result of dropping that condition, A, B and C can be any number. Since a,b,c do not have to be the same, each of A, B and C can be manipulated by multiplying by a sufficient constant in the form of e^a/b/c to fullfill the equation. Thus there should be atleast one set of a,b,c so that the identity holds true.

Sy123 · May 26, 2014

Re: HSC 2014 4U Marathon

Ikki said:
i) From the condition given, A+B=C.
Multiply everything by e^x. Ae^x+Be^x=Ce^x.
Now the only way to reach the * form is to multiply throughout by the same constant which in this case means that a=b=c must hold true.

ii) As a result of dropping that condition, A, B and C can be any number. Since a,b,c do not have to be the same, each of A, B and C can be manipulated by multiplying by a sufficient constant in the form of e^a/b/c to fullfill the equation. Thus there should be atleast one set of a,b,c so that the identity holds true.

Hmmm yea that looks right I guess, though your wording in the last sentence of your first answer is a little vague.

Rather I would say:

$Ce^x = Ae^x + Be^x$

$\Rightarrow \ Ce^{cx} = Ae^{cx} + Be^{cx}$

Thus, the only solutions (a,b) such that $Ae^{ax} + Be^{bx} = Ce^{cx}$ is when a=c, b=c, thus a=b=c

Sy123 · May 26, 2014

Re: HSC 2014 4U Marathon

$\\ $Let the series of complex numbers$ \ z_k = 1+ ik \ $for$ \ k=-n, -n+1, \dots, 0 , \dots, n-1, n \ $be in the Argand diagram$$

$\\ $Find the function$ \ f \ $so that the complex numbers$ \ f(z_k) \ $represent the corners of a$ \ (2n+1) \ $sided regular polygon$$

mathing · May 26, 2014

Re: HSC 2014 4U Marathon

Sy123 said:
$\\ $Let the series of complex numbers$ \ z_k = 1+ ik \ $for$ \ k=-n, -n+1, \dots, 0 , \dots, n-1, n \ $be in the Argand diagram$$

$\\ $Find the function$ \ f \ $so that the complex numbers$ \ f(z_k) \ $represent the corners of a$ \ (2n+1) \ $sided regular polygon$$

How about $f(z_k) = \exp(2\pi i($Im$(z_k)+n)/(2n+1))$ ?

Sy123 · May 26, 2014

Re: HSC 2014 4U Marathon

mathing said:
How about $f(z_k) = \exp(2\pi i($Im$(z_k)+n)/(2n+1))$ ?

Yea I guess that would work, I was expecting something to do with cis() but its the same thing

dunjaaa · Jun 3, 2014

Re: HSC 2014 4U Marathon

Volumes Question ->

Screen shot 2014-06-03 at 6.13.27 PM.png

aDimitri · Jun 3, 2014

Re: HSC 2014 4U Marathon

good question! took me a couple of minutes to wrap my head around what the solid looked like but then i realised it said the cross sections were perpendicular not parallel, and i felt like a fool

loving the volumes, it's definitely my favourite topic so far

EDIT: Started to LaTeX my solution, but cant be bothered, far too long.

mathing · Jun 8, 2014

Re: HSC 2014 4U Marathon

If you want to punish yourself have a go at this inequality:

$(lx + my + nz)^2 \le (l^2 + m^2 + n^2)(x^2 + y^2 + z^2)$

Ikki · Jun 8, 2014

Re: HSC 2014 4U Marathon

mathing said:
If you want to punish yourself have a go at this inequality:

$(lx + my + nz)^2 \le (l^2 + m^2 + n^2)(x^2 + y^2 + z^2)$

Not too hard:
Begin with expansions of:
(ly-mx)^2>=0
(nx-lz)^2>=0
(ny-mz)^2>=0

Then add them together to obtain:
l^2 * y^2 + l^2 * z^2 + m^2 * x^2 + m^2 * z^2 + n^2 * x^2 + n^2 * y^2 >= 2(lxmy+lxnz+mgnz)

Add l^2 * x^2 + m^2 * y^2 + n^2 * z^2 to both sides and factorise to obtain the required expression.

mathing · Jun 8, 2014

Re: HSC 2014 4U Marathon

You got it!

Ikki said:
Not too hard:
Begin with expansions of:
(ly-mx)^2>=0
(nx-lz)^2>=0
(ny-mz)^2>=0

Then add them together to obtain:
l^2 * y^2 + l^2 * z^2 + m^2 * x^2 + m^2 * z^2 + n^2 * x^2 + n^2 * y^2 >= 2(lxmy+lxnz+mgnz)

Add l^2 * x^2 + m^2 * y^2 + n^2 * z^2 to both sides and factorise to obtain the required expression.

Sy123 · Jun 8, 2014

Re: HSC 2014 4U Marathon

$\\ $Let$ \ a,b \ $is real, and such that$ \ \ \frac{a+b}{a-b} + \frac{a-b}{a+b} = 6 \ $and$ \ |a| \neq |b| \\ \\ $Find the value of$ \\ \\ \frac{a^3+b^3}{a^3-b^3} + \frac{a^3-b^3}{a^3+b^3}$

HSC 2014 MX2 Marathon (archive) (5 Viewers)

Active Member

This too shall pass

Active Member

Active Member

Active Member

Active Member

Active Member

Active Member

This too shall pass

Active Member

This too shall pass

This too shall pass

New Member

This too shall pass

Active Member

i'm the cook

New Member

Active Member

New Member

This too shall pass

Users Who Are Viewing This Thread (Users: 0, Guests: 5)