Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2014 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Re: HSC 2014 4U Marathon
Find the volume of the region bounded by the curve y=sin(x) between x=0 and x=pi rotated about the line y=-x.
If anyone else has any good oblique rotation questions, please share! It's in my upcoming assessment task even though its not in the syllabus and there isn't many questions I can source out from past papers or textbooks.
Find the volume of the region bounded by the curve y=sin(x) between x=0 and x=pi rotated about the line y=-x.
If anyone else has any good oblique rotation questions, please share! It's in my upcoming assessment task even though its not in the syllabus and there isn't many questions I can source out from past papers or textbooks.
Re: HSC 2014 4U Marathon
PHP:
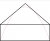
I know right? Basically inside the house which apparently has nothing in it. At one end of the house it is fired and hits one side of the triangular shaped roof and then reaches its maximum and hits the other side and then falls to finish at the other side of the house. That is why the range is the length of the house.Can you provide us with a diagram, because I can't translate your instructions into one lol (idk if we have different interpretations of the way a house looks like)
Re: HSC 2014 4U Marathon

Well maybe its a dog houseI know right? Basically inside the house which apparently has nothing in it. At one end of the house it is fired and hits one side of the triangular shaped roof and then reaches its maximum and hits the other side and then falls to finish at the other side of the house. That is why the range is the length of the house.PHP:
Re: HSC 2014 4U Marathon
i) From the condition given, A+B=C.
Multiply everything by e^x. Ae^x+Be^x=Ce^x.
Now the only way to reach the * form is to multiply throughout by the same constant which in this case means that a=b=c must hold true.
ii) As a result of dropping that condition, A, B and C can be any number. Since a,b,c do not have to be the same, each of A, B and C can be manipulated by multiplying by a sufficient constant in the form of e^a/b/c to fullfill the equation. Thus there should be atleast one set of a,b,c so that the identity holds true.
i) From the condition given, A+B=C.
Multiply everything by e^x. Ae^x+Be^x=Ce^x.
Now the only way to reach the * form is to multiply throughout by the same constant which in this case means that a=b=c must hold true.
ii) As a result of dropping that condition, A, B and C can be any number. Since a,b,c do not have to be the same, each of A, B and C can be manipulated by multiplying by a sufficient constant in the form of e^a/b/c to fullfill the equation. Thus there should be atleast one set of a,b,c so that the identity holds true.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
Rather I would say:


Thus, the only solutions (a,b) such that is when a=c, b=c, thus a=b=c
is when a=c, b=c, thus a=b=c
Hmmm yea that looks right I guess, though your wording in the last sentence of your first answer is a little vague.i) From the condition given, A+B=C.
Multiply everything by e^x. Ae^x+Be^x=Ce^x.
Now the only way to reach the * form is to multiply throughout by the same constant which in this case means that a=b=c must hold true.
ii) As a result of dropping that condition, A, B and C can be any number. Since a,b,c do not have to be the same, each of A, B and C can be manipulated by multiplying by a sufficient constant in the form of e^a/b/c to fullfill the equation. Thus there should be atleast one set of a,b,c so that the identity holds true.
Rather I would say:
Thus, the only solutions (a,b) such that
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
Yea I guess that would work, I was expecting something to do with cis() but its the same thingHow about?
aDimitri
i'm the cook
Re: HSC 2014 4U Marathon
good question! took me a couple of minutes to wrap my head around what the solid looked like but then i realised it said the cross sections were perpendicular not parallel, and i felt like a fool
loving the volumes, it's definitely my favourite topic so far
EDIT: Started to LaTeX my solution, but cant be bothered, far too long.
good question! took me a couple of minutes to wrap my head around what the solid looked like but then i realised it said the cross sections were perpendicular not parallel, and i felt like a fool
loving the volumes, it's definitely my favourite topic so far
EDIT: Started to LaTeX my solution, but cant be bothered, far too long.
Last edited:
Re: HSC 2014 4U Marathon
Begin with expansions of:
(ly-mx)^2>=0
(nx-lz)^2>=0
(ny-mz)^2>=0
Then add them together to obtain:
l^2 * y^2 + l^2 * z^2 + m^2 * x^2 + m^2 * z^2 + n^2 * x^2 + n^2 * y^2 >= 2(lxmy+lxnz+mgnz)
Add l^2 * x^2 + m^2 * y^2 + n^2 * z^2 to both sides and factorise to obtain the required expression.
Not too hard:If you want to punish yourself have a go at this inequality:
^2 \le (l^2 + m^2 + n^2)(x^2 + y^2 + z^2))
Begin with expansions of:
(ly-mx)^2>=0
(nx-lz)^2>=0
(ny-mz)^2>=0
Then add them together to obtain:
l^2 * y^2 + l^2 * z^2 + m^2 * x^2 + m^2 * z^2 + n^2 * x^2 + n^2 * y^2 >= 2(lxmy+lxnz+mgnz)
Add l^2 * x^2 + m^2 * y^2 + n^2 * z^2 to both sides and factorise to obtain the required expression.
Re: HSC 2014 4U Marathon
You got it!
You got it!
Not too hard:
Begin with expansions of:
(ly-mx)^2>=0
(nx-lz)^2>=0
(ny-mz)^2>=0
Then add them together to obtain:
l^2 * y^2 + l^2 * z^2 + m^2 * x^2 + m^2 * z^2 + n^2 * x^2 + n^2 * y^2 >= 2(lxmy+lxnz+mgnz)
Add l^2 * x^2 + m^2 * y^2 + n^2 * z^2 to both sides and factorise to obtain the required expression.
- Status
- Not open for further replies.