Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
Using the Integral test, prove the following limit:
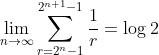
You may assume uniform convergence and the squeeze theorem.
Using the Integral test, prove the following limit:
You may assume uniform convergence and the squeeze theorem.
Last edited: