leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: Multivariable Calculus
My notes were really ambiguous. They just recited the chain rule except replaced all the u's and v's with r's and theta's and I have no idea how to manipulate it.
I attempted the matrix inverse as an exercise for myself in the meantime and I got this:
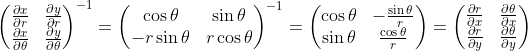
The last step was using what the answers were trying to tell me to prove. I don't actually know that the last step is true.
But I don't get the logic behind it.
These are my notes. Explanations would be greatly appreciated but because idk if the notes are copyrighted I probably can't keep them up for too long.
(Apparently, according to my lecturer, this has never been examined in first year before either...)
My notes were really ambiguous. They just recited the chain rule except replaced all the u's and v's with r's and theta's and I have no idea how to manipulate it.
I attempted the matrix inverse as an exercise for myself in the meantime and I got this:
The last step was using what the answers were trying to tell me to prove. I don't actually know that the last step is true.
But I don't get the logic behind it.
These are my notes. Explanations would be greatly appreciated but because idk if the notes are copyrighted I probably can't keep them up for too long.
(Apparently, according to my lecturer, this has never been examined in first year before either...)
Last edited:
