Higher Level Integration Marathon & Questions (3 Viewers)

omegadot · Feb 24, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
Nice excercise for manipulating special functions.

$$\noindent $ \int_0^\infty \text{erfc}(x)^2 \text{d}x \\\\ $Where erfc$(x)$ is the complementary error function.$ \\\\ $erfc$(x) = \frac{2}{\sqrt{\pi}}\int_{x}^\infty e^{-t^2} \text{d}t$

$\noindent We begin with a few preliminary results that I will make use of in my derivation.$

$\int^\infty_0 e^{-x^2} \, dx = \frac{\sqrt{\pi}}{2}$ (the Gaussian integral)$$

$\int^\infty_0 e^{-2x^2} \, dx = \frac{\sqrt{\pi}}{2\sqrt{2}}$ (Substitute $u = t/\sqrt{2}$ in the above integral)$$

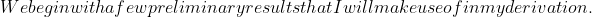
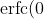$\text{erfc}(0) = 1, \frac{d}{dx} \text{erfc}(x) = -\frac{2}{\sqrt{\pi}} e^{-x^2}$

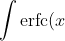$\int \text{erfc}(x) \, dx = x \text{erfc}(x) - \frac{1}{\sqrt{\pi}} e^{-x^2} + \mathcal{C}$ (established using IBP)$$

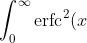$\noindent Now writing the integral as$

$\int_0^\infty \text{erfc}^2(x) \, dx = \int_0^\infty \text{erfc}(x) \cdot \text{erfc}(x) \, dx.$

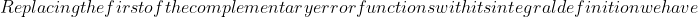
$\noindent Replacing the first of the complementary error functions with its integral definition we have$

$\begin{align*}\int_0^\infty \text{erfc}^2(x) \, dx &=\int_0^\infty \frac{2}{\sqrt{\pi}} \int^\infty_x e^{-u^2} \, du \cdot \text{erfc}(x) \, dx\\&=\frac{2}{\sqrt{\pi}} \int^\infty_0 \int^\infty_x e^{-u^2} \text{erfc}(x) \, du \,dx\\&=\frac{2}{\sqrt{\pi}}\int^\infty_0 \int^u_0 e^{-u^2} \text{erfc}(x) \, dx\,du,\end{align*}$

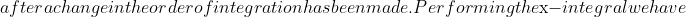
$\noindent after a change in the order of integration has been made. Performing the $x$-integral we have$

$\begin{align*}\int_0^\infty \text{erfc}^2(x) \, dx &=\frac{2}{\sqrt{\pi}} \int^\infty_0 e^{-u^2} \left [x \text{erfc}(x) - \frac{1}{\sqrt{\pi}} e^{-x^2} \right ]^u_0 \, du\\&= \frac{2}{\sqrt{\pi}} \int^\infty_0 e^{-u^2} \left [u \text{erfc}(u) - \frac{1}{\sqrt{\pi}} e^{-u^2} + \frac{1}{\sqrt{\pi}} \right ] \, du\\&=\frac{2}{\sqrt{\pi}}\int^\infty_0 ue^{-u^2} \cdot \text{erfc}(u) \, du - \frac{2}{\pi} \int^\infty_0 e^{-2u^2} \, du + \frac{2}{\pi} \int^\infty_0 e^{-u^2} \, du\end{align*}$

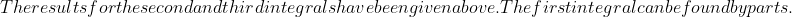
$\noindent The results for the second and third integrals have been given above. The first integral can be found by parts.$

$\begin{align*}\int^\infty_0 ue^{-u^2} \cdot \text{erfc}(u) \, du &= -\frac{1}{2} e^{-u^2} \text{erfc}(u) \Big{|}^\infty_0 - \int^\infty_0 -\frac{1}{2} e^{-u^2} \cdot -\frac{2}{\sqrt{\pi}} e^{-u^2} \, du\\ &= \frac{1}{2} - \frac{1}{\sqrt{\pi}} \int^\infty_0 e^{-2u^2} \, du\\&= \frac{1}{2} - \frac{1}{\sqrt{\pi}} \cdot \frac{\sqrt{\pi}}{2\sqrt{2}}\\&=\frac{1}{2} - \frac{1}{2\sqrt{2}}.\end{align*}$

$\noindent Thus$

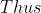
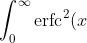$\int_0^\infty \text{erfc}^2(x) \, dx = \frac{2}{\sqrt{\pi}} \left (\frac{1}{2} - \frac{1}{2\sqrt{2}} \right ) - \frac{2}{\pi} \cdot \frac{\sqrt{\pi}}{2 \sqrt{2}} + \frac{2}{\pi} \cdot \frac{\sqrt{\pi}}{2} = \frac{2 - \sqrt{2}}{\sqrt{\pi}}.$

omegadot · Feb 27, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
Here's an easier one. Fun Exercise

$\noindent \int_0^1 \frac{\tan^{-1}{x}\text{d}x}{x\sqrt{1-x^2}}$

$$\noindent In our solution we will make use of the following two Maclaurin series expansions$

$\tan^{-1} t = \sum^\infty_{n = 0} \frac{(-1)^n t^{2n + 1}}{2n + 1}, \, |t| < 1 $ and $\,\sinh^{-1} t = \sum^\infty_{n = 0} \frac{(-1)^n (2n)! t^{2n + 1}}{(2n + 1) 2^{2n} (n!)^2}, \,\, |t| \leqslant 1.$

$$\noindent Making the substitution $x = \sin \theta$ in the integral. Thus $dx = \cos \theta \, d\theta$ and for the limits of integration, when $x = 0, \theta = 0$ and as $x \to \infty, \theta \to \frac{\pi^-}{2}. $ Thus$

$\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx = \int^{\frac{\pi}{2}}_0 \frac{\tan^{-1} (\sin \theta)}{\sin \theta} \, d\theta.$

$\noindent Setting $t = \sin \theta$ in the Maclaurin series expansion for the inverse tangent function and replacing this term in the integral, after interchanging the order of the summation with the integration we have$

$\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx = \sum^\infty_{n = 0} \frac{(-1)^n}{2n + 1} \int^{\frac{\pi}{2}}_0 \sin^{2n} \theta \, d\theta.$

$\noindent The sine integral appearing here is well known. The result is$

$\int^{\frac{\pi}{2}}_0 \sin^{2n} \theta \, d\theta = \frac{\pi(2n)!}{2^{2n + 1} (n!)^2}.$

$\noindent Thus$

$\begin{align*}\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx &= \sum^{\infty}_{n = 0} \frac{(-1)^n \pi (2n)!}{(2n + 1) 2^{2n + 1} (n!)^2}\\&= \frac{\pi}{2} \sum^\infty_{n = 0} \frac{(-1)^n (2n)!}{(2n + 1) 2^{2n} (n!)^2} = \frac{\pi}{2} \sinh^{-1} (1),\end{align*}$

$\noindednt as required to show.$

omegadot · Feb 27, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
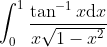
A fairly easy exercise.

$\int_{-\infty}^{\infty} \frac{\cos{ax} - \cos{bx}}{x^2} $d$x$, where ${a,b} \in \mathbb{R}^+$

$\noindent In order to evaluate this integral we will convert it into a double integral. Observing that$

$\int^b_a \sin (ux) \, du = \frac{\cos (ax) - \cos (bx)}{x}, $ the integral can be rewritten as$$

$\begin{align*}\int^\infty_{-\infty}\frac{\cos (ax) - \cos (bx)}{x^2} \, dx &= \int^\infty_{-\infty} \int^b_a \frac{\sin (ux)}{x} \, du \, dx\\&= \int^b_a \int^\infty_{-\infty} \frac{\sin (ux)}{x} \, dx \, du,\end{align*}$

$\noindent after a change in the order of integration is made. Now let $t = ux, dt = u \, dx $ while the $x$-limits of integration remain unchanged. Thus$

$\int^\infty_{-\infty}\frac{\cos (ax) - \cos (bx)}{x^2} \, dx = \int^b_a \int^\infty_{-\infty} \frac{\sin t}{t} \, dt \, du.$

$\noindent Now the \textit{Dirichlet integral} has been previously found in this thread. The result is$

$\int^\infty_{-\infty} \frac{\sin t}{t} \, dt = \pi.$

$\noindent So finally$

$\int^\infty_{-\infty}\frac{\cos (ax) - \cos (bx)}{x^2} \, dx = \pi \int^b_a du = \pi(b - a).$

omegadot · Feb 27, 2017

Re: Extracurricular Integration Marathon

$$\noindent \textbf{New Question}$

$$\noindent Evaluate $\int^{\frac{\pi}{2}}_0 \ln \left (\frac{1 + \sin x}{1 - \sin x} \right ) \frac{\cos^2 x}{\sin x} \, dx.$

Paradoxica · Feb 27, 2017

Re: Extracurricular Integration Marathon

omegadot said:
$$\noindent In our solution we will make use of the following two Maclaurin series expansions$

$\tan^{-1} t = \sum^\infty_{n = 0} \frac{(-1)^n t^{2n + 1}}{2n + 1}, \, |t| < 1 $ and $\,\sinh^{-1} t = \sum^\infty_{n = 0} \frac{(-1)^n (2n)! t^{2n + 1}}{(2n + 1) 2^{2n} (n!)^2}, \,\, |t| \leqslant 1.$

$$\noindent Making the substitution $x = \sin \theta$ in the integral. Thus $dx = \cos \theta \, d\theta$ and for the limits of integration, when $x = 0, \theta = 0$ and as $x \to \infty, \theta \to \frac{\pi^-}{2}. $ Thus$

$\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx = \int^{\frac{\pi}{2}}_0 \frac{\tan^{-1} (\sin \theta)}{\sin \theta} \, d\theta.$

$\noindent Setting $t = \sin \theta$ in the Maclaurin series expansion for the inverse tangent function and replacing this term in the integral, after interchanging the order of the summation with the integration we have$

$\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx = \sum^\infty_{n = 0} \frac{(-1)^n}{2n + 1} \int^{\frac{\pi}{2}}_0 \sin^{2n} \theta \, d\theta.$

$\noindent The sine integral appearing here is well known. The result is$

$\int^{\frac{\pi}{2}}_0 \sin^{2n} \theta \, d\theta = \frac{\pi(2n)!}{2^{2n + 1} (n!)^2}.$

$\noindent Thus$

$\begin{align*}\int^1_0 \frac{\tan^{-1} x}{x\sqrt{1 - x^2}} \, dx &= \sum^{\infty}_{n = 0} \frac{(-1)^n \pi (2n)!}{(2n + 1) 2^{2n + 1} (n!)^2}\\&= \frac{\pi}{2} \sum^\infty_{n = 0} \frac{(-1)^n (2n)!}{(2n + 1) 2^{2n} (n!)^2} = \frac{\pi}{2} \sinh^{-1} (1),\end{align*}$

$\noindednt as required to show.$

That's nice but it's not exactly an answer, since you haven't proven that the sum is the inverse hyperbolic sine of 1.

InteGrand · Feb 27, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
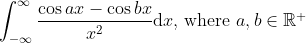
That's nice but it's not exactly an answer, since you haven't proven that the sum is the inverse hyperbolic sine of 1.

He used the Maclaurin series for the inverse hyperbolic sine (and the fact it holds at t = 1, which we can show for example by using Abel's theorem. We can show the series converges with the help of Stirling's approximation, for example).

Paradoxica · Feb 27, 2017

Re: Extracurricular Integration Marathon

omegadot said:
$$\noindent \textbf{New Question}$

$$\noindent Evaluate $\int^{\frac{\pi}{2}}_0 \ln \left (\frac{1 + \sin x}{1 - \sin x} \right ) \frac{\cos^2 x}{\sin x} \, dx.$

The logarithmic component can be reverted into an integral as follows:

$\int_0^1 \frac{2\sin{x} \, \text{d}a}{1-a^2\sin^2{x}} = \log{\left(\frac{1+\sin{x}}{1-\sin{x}}\right)}$

Note that both integrals are finite and bounded. By Tonelli's Theorem, the reversion and interchange are valid operations.

$$\noindent$ \int^{\frac{\pi}{2}}_0 \log \left (\frac{1 + \sin x}{1 - \sin x} \right ) \frac{\cos^2 x}{\sin x} \, dx = \int_0^1 \int_0^\frac{\pi}{2} \frac{2\cos^2{x}\,\text{d}x}{1-a^2\sin^2{x}} \, \text{d}a \\\\ = \int_0^1 \frac{\pi \, \text{d}a}{(1+\sqrt{1-a^2})} = \pi\left(\frac{\pi}{2}-1\right)$

omegadot · Feb 28, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
Another exercise:

$\int_{-\infty}^\infty \frac{a \sin{b x} - b \sin{ax} }{x^3}$d$x \quad \{a,b\} \in \mathbb{R}^+$

$$\noindent In this question the following result previously found will be used$

$\int^\infty_{-\infty} \frac{\cos ax - \cos bx}{x^2} \, dx = \pi (b - a), \quad \{a,b\} \in \mathbb{R}^+$

$\noindent Integrating by parts we have$

$\int^\infty_{-\infty} \frac{a \sin bx - b \sin ax}{x^3} \, dx = -\frac{ab}{2} \int^\infty_{-\infty} \frac{\cos ax - \cos bx}{x^2} \, dx = \frac{ab (a- b)\pi}{2}.$

omegadot · Feb 28, 2017

Re: Extracurricular Integration Marathon

KingOfActing said:
$\int_{-\infty}^{\infty} \frac{\sin^2{x}}{1+x^2}\,dx$

$\noindent In this question the following result will be used:$

$\int^\infty_0 \frac{\sin ax}{x} \, dx = \left \{\begin{align*}\frac{\pi}{2}, \quad a > 0\\[2ex]-\frac{\pi}{2}, \quad a< 0.\end{align*}\right.$

$\noindent Now$

$\begin{align*}\int^\infty_{-\infty} \frac{\sin^2 x}{1 + x^2} \, dx &= 2\int^\infty_0 \frac{\sin^2 x}{1 + x^2} \, dx \quad \mbox{(is even)}\\ &=\int^\infty_0 \frac{1 - \cos 2x}{1 + x^2} \, dx\\ &= \int^\infty_0 \frac{dx}{1 + x^2} - \int^\infty_0 \frac{\cos 2x}{1 + x^2} \, dx\\ &= \frac{\pi}{2} -2\int^\infty_0 \frac{\cos u}{4 + u^2} \, du \quad \mbox{(setting} \,\, 2x = u)\end{align*}$

$\noindent Now consider the integral containing the cosine term. Using integration by parts twice, we observe that$

$\int^\infty_0 e^{-2t} \sin (ut) \, dt = \frac{u}{4 + u^2}.$

$\noindent (Yes, I know. So how on Earth does one recognise this? Well, it turns out it is just the Laplace transform for sine.)$

$\noindent So we can rewrite the integral containing the cosine term as$

$\begin{align*}\int^\infty_0 \frac{\cos u}{4 + u^2} \, du &= \int^\infty_0 \frac{\cos u}{u} \cdot \frac{u}{4 + u^2} \, du\\ &=\int^\infty_0 \int^\infty_0 e^{-2t} \, \frac{\cos u \sin ut}{u} \, du \, dt \quad \mbox{(after a change of order)}\end{align*}$

$\noindent Since $\cos u \sin ut = \frac{1}{2} \sin (t + 1)u + \frac{1}{2} \sin (t - 1) u,$ the above integral may be rewritten as$

$\int^\infty_0 \frac{\cos u}{4 + u^2} \, du = \frac{1}{2} \int^\infty_0 e^{-2t} \int^\infty_0 \left [\frac{\sin (t + 1)u}{u} + \frac{\sin (t - 1)u}{u} \right ] \, du \, dt.$

$\noindent Now, for the two integrals which appear in terms of sine we have$

$\int^\infty_0 \frac{\sin (t - 1) u}{u} \, du = \frac{\pi}{2},$ for all $t \geqslant 0.$

$\noindent and$

$\int^\infty_0 \frac{\sin (t + 1)u}{u} \, du = \left \{\begin{align*} \frac{\pi}{2}, \quad t > 1\\[2ex] -\frac{\pi}{2}, \quad t < 1\end{align*}\right.$

$\noindent So$

$\int^\infty_0 \frac{\cos u}{4 + u^2} \, du = \frac{\pi}{2} \int^\infty_1 e^{-2t} \, dt = \frac{\pi}{4} e^{-2}$

$\noindent Giving$

$\int^\infty_{-\infty} \frac{\sin^2 x}{1 + x^2} \, dx = \frac{\pi}{2} - \frac{\pi}{2e^2} = \frac{\pi}{e} \sinh (1).$

omegadot · Feb 28, 2017

Re: Extracurricular Integration Marathon

$$\noindent Using real methods only, evaluate $\int^\infty_0 \frac{\sqrt{x}}{(1 + x)^2} \ln x \, dx.$

Paradoxica · Feb 28, 2017

Re: Extracurricular Integration Marathon

omegadot said:
$$\noindent Using real methods only, evaluate $\int^\infty_0 \frac{\sqrt{x}}{(1 + x)^2} \ln x \, dx.$

Real Methods, you say?

$$\noindent$ \int_0^\infty \frac{\sqrt{x}}{(1+x)^2} \log{x} \, \text{d}x = \frac{\text{d}}{\text{d} a} \left. \int_0^\infty \frac{x^a}{(1+x)^2} \, \text{d}x \right|_{a=\frac{1}{2}} = \frac{\text{d}}{\text{d}a} \left. \text{B}(a+1,1-a) \right|_{a=\frac{1}{2}} \\\\ = \frac{\text{d}}{\text{d}a} \left. \frac{\Gamma(a+1) \Gamma(1-a)}{\Gamma(2)} \right|_{a=\frac{1}{2}} = \frac{\text{d}}{\text{d}a} \left. \frac{\pi a}{\sin{\pi a}} \right|_{a=\frac{1}{2}} = \frac{\pi}{\sin{\frac{\pi}{2}}} - \frac{\frac{\pi^2}{2}\cos{\frac{\pi}{2}}}{ \sin^2{ \frac{\pi}{2} } } = \pi$

omegadot · Mar 1, 2017

Re: Extracurricular Integration Marathon

Paradoxica said:
Prove the following result:

$\int_0^\infty \frac{(x^2-1)\tan^{-1}{(x^2)}}{x^4 + 4x^2 +1}$d$x= \frac{\pi^2}{12\sqrt{2}}$

$\noindent I have a solution for this one, but given it is quite long, I will break it down into a number of parts.$

$\noindent Paradoxia - If you have a shorter or more elegant solution compared to what I am about to give, please share it with the rest of us.$

$\noindent \textbf{Part I}$

$\noindent We show that $\int \frac{x^2 - 1}{1 + 4x^2 + x^4} \, dx = \alpha \tan^{-1} \left (\frac{x}{a} \right ) - \beta \tan^{-1} \left (\frac{x}{b} \right ) + \mathcal{C}$ where,$

$\alpha = \frac{(\sqrt{3} - 1) \sqrt{2 + \sqrt{3}}}{2}, \quad \beta = \frac{(\sqrt{3} + 1) \sqrt{2 - \sqrt{3}}}{2},$

$a = \sqrt{2 + \sqrt{3}}, \quad b = \sqrt{2 - \sqrt{3}}.$

$\noindent Noting that $1 + 4x^2 + x^4 = [(2 + \sqrt{3})x^2 + 1][(2 - \sqrt{3}) x^2 + 1], $then the partial fraction decomposition for $\frac{x^2 - 1}{1 + 4x^2 + x^4}$ is$

$\begin{align*}\frac{x^2 - 1}{1 + 4x^2 + x^4} &= \frac{x^2 - 1}{[(2 + \sqrt{3})x^2 + 1][(2 - \sqrt{3}) x^2 + 1]}\\ &= \frac{\sqrt{3} - 1}{2[(2 - \sqrt{3})x^2 + 1]} - \frac{\sqrt{3} + 1}{2[(2 + \sqrt{3})x^2 + 1]}.\end{align*}$

$\noindent Thus $\int \frac{x^2 - 1}{1 + 4x^2 + x^4} \, dx = \alpha \tan^{-1} \left (\frac{x}{a} \right ) - \beta \tan^{-1} \left (\frac{x}{b} \right ) + \mathcal{C}$ readily follows after performing the integrations and a little algebra.$

$\noindent \textbf{Part II}$

$\noindent Next we show that$

$I(s) = \int^\infty_0 \frac{x}{x^4 + 1} \tan^{-1} \left (\frac{x}{s} \right ) \, dx = \frac{\pi^2}{4} - \frac{\pi}{2} \tan^{-1} (s\sqrt{2} + 1), \,\, s > 0.$

$$\noindent Recognising that for $s,x > 0$

$\int^s_0 \frac{dy}{y^2 + x^2} = \frac{1}{x} \tan^{-1} \left (\frac{s}{x} \right ) = \frac{\pi}{2x} - \frac{1}{x} \tan^{-1} \left (\frac{x}{a} \right ),$

$\noindent where use of the result $\tan^{-1} u + \tan^{-1} \frac{1}{u} = \frac{\pi}{2}, u > 0$ has been made. So we can write$

$\tan^{-1} \left (\frac{x}{s} \right ) = \frac{\pi}{2} - x \int^s_0 \frac{dy}{y^2 + x^2}.$

$\noindent Now, for our integral it can be rewritten as$

$\begin{align*}I(s) &= \int^\infty_0 \frac{x}{x^4 + 1} \tan^{-1} \left (\frac{x}{s} \right ) \, dx\\ &= \frac{\pi}{2} \int^\infty_0 \frac{x}{x^4 + 1} \, dx - \int^\infty_0 \int^s_0 \frac{x^2}{x^4 + 1} \cdot \frac{1}{y^2 + x^2} \, dy \, dx\\&= \frac{\pi^2}{8} - \int^s_0 \int^\infty_0 \frac{x^2}{x^4 + 1} \cdot \frac{1}{y^2 + x^2} \, dx \, dy,\end{align*}$

$\noindent after a change in the order of integration has been made.$

$\noindent For the rational function in terms of $x$, performing a partial fraction decomposition one has$

$\frac{x^2}{(x^4 + 1)(y^2 + x^2)} = \frac{1}{(y^4 + 1)(x^4 + 1)} - \frac{y^2}{(y^4 + 1)(y^2 + x^2)} + \frac{y^2 x^2}{(y^4 + 1)(x^4 + 1)}.$

$\noindent So for the $x$-integral we have$

$\begin{align*}\int^\infty_0 \frac{x^2}{x^4 + 1} \cdot \frac{1}{y^2 + x^2} \, dx &= \frac{1}{y^4 + 1} \int^\infty_0 \frac{dx}{x^4 + 1} - \frac{y^2}{y^4 + 1} \int^\infty_0 \frac{dx}{y^2 + x^2} + \frac{y^2}{y^4 + 1} \int^\infty_0 \frac{x^2}{x^4 + 1} \, dx\\&= \frac{1}{y^4 + 1} \cdot \frac{\pi}{2\sqrt{2}} - \frac{y^2}{y^4 + 1} \cdot \frac{\pi}{2y} + \frac{y^2}{y^4 + 1} \cdot \frac{\pi}{2 \sqrt{2}}\\&=\frac{\pi}{2\sqrt{2}} \frac{y^2 - y\sqrt{2} + 1}{y^4 + 1}\\&=\frac{\pi}{2\sqrt{2}} \frac{y^2 - y\sqrt{2} + 1}{(y^2 + y\sqrt{2} + 1)(y^2 - y\sqrt{2} + 1)}\\&= \frac{\pi}{2\sqrt{2}} \frac{1}{y^2 + y\sqrt{2} + 1}.\end{align*}$

$\noindent Thus$

$\begin{align*}I(s) &= \frac{\pi^2}{8} - \frac{\pi}{2\sqrt{2}} \int^s_0 \frac{dy}{y^2 + y\sqrt{2} + 1}\\&= \frac{\pi^2}{8} - \frac{\pi}{2} \tan^{-1} (y\sqrt{2} + 1) \Big{|}^s_0\\&= \frac{\pi^2}{4} - \frac{\pi}{2} \tan^{-1} (s\sqrt{2} + 1).\end{align*}$

$\noindent \textbf{Part III}$

$\noindent We now prove the main result. Noting that $\frac{d}{dx} \left [\tan^{-1} (x^2) \right ] = \frac{2x}{1 + x^4}$ using integration by parts we have$

$\begin{align*}\int^\infty_0 \frac{(x^2 - 1) \tan^{-1} (x^2)}{1 + 4x^2 + x^4} \, dx &= \left [\alpha \tan^{-1} \left (\frac{x}{a} \right ) - \beta \tan^{-1} \left (\frac{x}{b} \right ) \right ] \tan^{-1} (x^2) \Big{|}^\infty_0 - \int^\infty_0 \frac{2x}{1 + x^4} \left [\alpha \tan^{-1} \left (\frac{x}{a} \right ) - \beta \tan^{-1} \left (\frac{x}{b} \right ) \right ] \, dx\\&= (\alpha - \beta) \frac{\pi^2}{4} - 2\alpha \int^\infty_0 \frac{x}{1 + x^4} \tan^{-1} \left (\frac{x}{a} \right ) \, dx + 2\beta \int^\infty_0 \frac{x}{1 + x^4} \tan^{-1} \left (\frac{x}{b} \right ) \, dx\\&= (\alpha - \beta) \frac{\pi^2}{4} - 2\alpha I(a) - 2\beta I(b).\end{align*}$

$\noindent Now finding all necessary values:$

$I(a) = I(\sqrt{2 + \sqrt{3}}) = \frac{\pi^2}{4} - \frac{\pi}{2} \tan^{-1} (\sqrt{4 + 2\sqrt{3}} + 1) = \frac{\pi^2}{4} - \frac{\pi}{2} \cdot \frac{5\pi}{12} = \frac{\pi^2}{24}.$

$I(b) = I(\sqrt{2 - \sqrt{3}}) = \frac{\pi^2}{4} - \frac{\pi}{2} \tan^{-1} (\sqrt{4 - 2\sqrt{3}} + 1) = \frac{\pi^2}{4} - \frac{\pi}{2} \cdot \frac{\pi}{3} = \frac{\pi^2}{12}.$

$\noindent Thus$

$\begin{align*}\int^\infty_0 \frac{(x^2 - 1) \tan^{-1} (x^2)}{1 + 4x^2 + x^4} \, dx &= (\alpha - \beta) \frac{\pi^2}{4} - \alpha \frac{\pi^2}{12} + \beta \frac{\pi^2}{6}\\&= \frac{\pi^2}{6} \alpha - \frac{\pi^2}{12} \beta\\&= \frac{\pi^2 (\sqrt{3} - 1)\sqrt{2 + \sqrt{3}}}{12} - \frac{\pi^2 (\sqrt{3} + 1)\sqrt{2 - \sqrt{3}}}{24}\\&= \frac{\pi^2}{12 \sqrt{2}},\end{align*}$

$\noindent as required to show!!$

Paradoxica · Mar 1, 2017

Re: Extracurricular Integration Marathon

omegadot said:
$\noindent I have a solution for this one, but given it is quite long, I will break it down into a number of parts.$

$\noindent Paradoxica - If you have a shorter or more elegant solution compared to what I am about to give, please share it with the rest of us.$

There's only contour integration which is what I didn't want XD. Thanks for this completely elementary solution which I have been desiring for a long time.

Paradoxica · Mar 3, 2017

Re: Extracurricular Integration Marathon

Evaluate :

$\int_0^\frac{\pi}{2} \log{(a^2\cos^2{x}+b^2\sin^2{x})} \, \text{d}x$

In at least 3 different ways.

seanieg89 · Mar 5, 2017

Re: Extracurricular Integration Marathon

One way (probably pretty inefficient so am not going to bother texing it) is to just differentiate with respect to the parameters.

I let x=a^2, y=b^2, and evaluated $\partial_xI(x,y)=\frac{\pi}{2(x-y)}\left(1-\frac{\sqrt{y}}{\sqrt{x}}\right)$ using the easy result that $\int_0^\pi \frac{d\theta}{a+\cos{\theta}}=\frac{\pi}{\sqrt{a^2-1}}$ for a > 1.

$\Rightarrow I(x,y)=I(y,y)+\int_y^x \partial_xI(t,y)\, dt=\pi \log(\sqrt{y})+\pi \log(\frac{\sqrt{x}+\sqrt{y}}{2\sqrt{y}}) \\=\pi\log(\frac{a+b}{2}).$

(And chuck some absolute values around a and b if you want to allow them to be negative obviously.)

Paradoxica · Mar 5, 2017

Re: Extracurricular Integration Marathon

seanieg89 said:
One way (probably pretty inefficient so am not going to bother texing it) is to just differentiate with respect to the parameters.

I let x=a^2, y=b^2, and evaluated $\partial_xI(x,y)=\frac{\pi}{2(x-y)}\left(1-\frac{\sqrt{y}}{\sqrt{x}}\right)$ using the easy result that $\int_0^\pi \frac{d\theta}{a+\cos{\theta}}=\frac{\pi}{\sqrt{a^2-1}}$ for a > 1.

$\Rightarrow I(x,y)=I(y,y)+\int_y^x \partial_xI(t,y)\, dt=\pi \log(\sqrt{y})+\pi \log(\frac{\sqrt{x}+\sqrt{y}}{2\sqrt{y}}) \\=\pi\log(\frac{a+b}{2}).$

(And chuck some absolute values around a and b if you want to allow them to be negative obviously.)

You could combine that with the symmetry of the integral to cut through some of that I suppose....

I(a,b) = I(b,a), from reflection.

Mahan1 · Mar 5, 2017

Re: HSC 2017 MX2 Integration Marathon

$\textrm{1.If} \ \alpha, \beta \ \textrm{ are real numbers such that}$
$\beta^{3} -6\beta^{2} + 13\beta = 19 , \ \alpha^{3}-6\alpha^{2} +13\alpha = 1$
$\textrm{Hence, find } \ (\alpha + \beta)$

$\textrm{2.If }f(x) = \frac{4^{x}}{4^{x}+2}$
$\textrm{Find} f(\frac{1}{14}) + ... + f(\frac{13}{14}) \ \textrm{without using calculator}$

pikachu975 · Mar 5, 2017

Re: HSC 2017 MX2 Integration Marathon

Mahan1 said:
$\textrm{If} \ \alpha, \beta \ \textrm{ are real numbers such that}$
$\beta^{3} -6\beta^{2} + 13\beta = 19 , \ \alpha^{3}-6\alpha^{2} +13\alpha = 1$
$\textrm{Hence, find } \ (\alpha + \beta)$

Add the two equations

B^3 + a^3 - 6B^2 - 6a^2 + 13B + 13a = 20
a^3 + B^3 - 6(B^2 + a^2) + 13(B+a) = 20
(a+B)(a^2 - aB + B^2) - 6(B^2 + a^2) + 13(B+a) = 20
(a+B)(a^2 - aB + B^2 - 6B^2 - 6a^2 + 13) = 20
(a+B)(-5a^2 - 5B^2 - aB + 13) = 20

Not sure what else to do but hopefully this helps someone but it probably won't

omegadot · Mar 10, 2017

Re: Extracurricular Integration Marathon

$$\noindent Evaluate (preferably using real methods) $\int^\infty_0 \frac{\ln x}{1 + x^3} \, dx.$

Paradoxica · Mar 11, 2017

Re: HSC 2017 MX2 Integration Marathon

Mahan1 said:
$\textrm{1.If} \ \alpha, \beta \ \textrm{ are real numbers such that}$
$\beta^{3} -6\beta^{2} + 13\beta = 19 , \ \alpha^{3}-6\alpha^{2} +13\alpha = 1$
$\textrm{Hence, find } \ (\alpha + \beta)$

Now that this is somewhere slightly more appropriate...

With the substitutions α = u+2, β = v+2, the following equations are obtained:

u³+u=-9, v³+v=9

f: x → x³+x is bijective, so there can only be one root.

Thus, u+v=0, since they have oppositely signed variables in the same equation.

Thus, α+β=4

Higher Level Integration Marathon & Questions (3 Viewers)

Active Member

Active Member

Active Member

Active Member

-insert title here-

Well-Known Member

-insert title here-

Active Member

Active Member

Active Member

-insert title here-

Active Member

-insert title here-

-insert title here-

Well-Known Member

-insert title here-

Member

Premium Member

Active Member

-insert title here-

Users Who Are Viewing This Thread (Users: 0, Guests: 3)