SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: HSC 2013 4U Marathon
1.
There are more elegant ways to do 1st integral Sy.
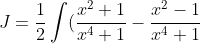)
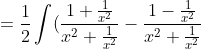\;dx)
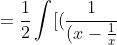^2+2}\;d(x-\frac{1}{x})}-\frac{1}{2}\int \frac{1}{(x+\frac{1}{x})^2-2}\;d(x+\frac{1}{x})])
You can either do it partial fracts or using the standard integrals not listed.
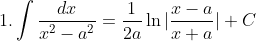
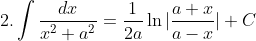
1.
There are more elegant ways to do 1st integral Sy.
You can either do it partial fracts or using the standard integrals not listed.
Last edited:

