Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (2 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Try the old version of the question now, you should be able to get it if you got that one.-pi/4?
Re: HSC 2013 4U Marathon
edit: oh right it can also be pi as well
0, since if all the coefficients are real, the roots must occur in conjugate pairs, therefore the arguments will be in opposite in sign?The quadratichas roots
+arg(\beta))
edit: oh right it can also be pi as well
Last edited:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
But the new version has complex co-efficients and the old version has real co-efficientsTry the old version of the question now, you should be able to get it if you got that one.
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
but he said in terms of a, b, c0, since if all the coefficients are real, the roots must occur in conjugate pairs, therefore the arguments will be in opposite in sign?
Well I meant find the argument in terms of a, b, c.
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
You can do it that way too, both answers are correct really.but he said in terms of a, b, c
Last edited:
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
0, since if all the coefficients are real, the roots must occur in conjugate pairs, therefore the arguments will be in opposite in sign?
edit: oh right it can also be pi as well if both roots are real but one's negative and other's positive.
0(a+b+c-3ab +2(a^2)b - c^3)=0 (that's in terms of a,b,c)but he said in terms of a, b, c
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
There's a much simpler expression lol.0(a+b+c-3ab +2(a^2)b - c^3)=0 (that's in terms of a,b,c)
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
How can it be pi as well?0, since if all the coefficients are real, the roots must occur in conjugate pairs, therefore the arguments will be in opposite in sign?
edit: oh right it can also be pi as well
Re: HSC 2013 4U Marathon
but then technically it can be -pi too
if the roots are real but one's negative and the other positive?How can it be pi as well?
but then technically it can be -pi too
RealiseNothing
what is that?It is Cowpea
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
It was a joke... Twink gave the answer as 0 and Herioc said it had to be in terms of a,b,c -> thus my answerThere's a much simpler expression lol.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: HSC 2013 4U Marathon
I'm impressed that the advertisement of this thread worked to a degree.
I'm impressed that the advertisement of this thread worked to a degree.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
oh lol, nvm then.It was a joke... Twink gave the answer as 0 and Herioc said it had to be in terms of a,b,c -> thus my answer
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,503
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
realise, diggin' the sig bro.oh lol, nvm then.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

And sum of them two at a time, then three at a time -> why not find a polynomial with roots 1/alpha 1/beta 1/gamma
And it actually isn't time consuming at all, in order to find a polynomial with those roots, you must 'reverse' the co-efficients
So a poly with roots 1/a 1/b 1/c
would be:
2x^3+3x^2+0x+1 = 0
So then you could find sum of them one at a time, two at a time and three by just using co-efficients instead of finding common denominator and going through that torturous process
And you could do the same for sum of squares and stuff as well.
Nice work, alternatively while we can do it your way, do you see how you needed to finddamn I think I missed all the shortcuts
And sum of them two at a time, then three at a time -> why not find a polynomial with roots 1/alpha 1/beta 1/gamma
And it actually isn't time consuming at all, in order to find a polynomial with those roots, you must 'reverse' the co-efficients
So a poly with roots 1/a 1/b 1/c
would be:
2x^3+3x^2+0x+1 = 0
So then you could find sum of them one at a time, two at a time and three by just using co-efficients instead of finding common denominator and going through that torturous process
And you could do the same for sum of squares and stuff as well.
Last edited:
Immortalp00n
Member
- Joined
- Dec 27, 2012
- Messages
- 272
- Gender
- Undisclosed
- HSC
- 2009
Re: HSC 2013 4U Marathon
i came to this thread for d babes as per sy's sig
where them bad bitches at?
i came to this thread for d babes as per sy's sig
where them bad bitches at?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

Only maths here, if that's what you're talking about.
Err, not sure what you're talking abouti came to this thread for d babes as per sy's sig
where them bad bitches at?
Only maths here, if that's what you're talking about.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Sorry about that.i came to this thread for d babes as per sy's sig
where them bad bitches at?
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
I was playing around with these sorts of problems on the bus the other day, but I ended up confusing myself and didn't get very far.
Say you had a polynomial with roots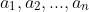 and you want to find a polynomial with roots
and you want to find a polynomial with roots 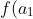, f(a_2), ..., f(a_n)) (Sy's question would be a special case of this where
(Sy's question would be a special case of this where  = x + \frac{1}{x}) ).
).
You can find an equation with these roots by replacing every instance of in the polynomial with
in the polynomial with 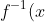) (this is an interesting property to investigate/prove). In some cases, that equation can be algebraically manipulated into a polynomial without creating any new roots. This is why the trick of inverting coefficients works for
(this is an interesting property to investigate/prove). In some cases, that equation can be algebraically manipulated into a polynomial without creating any new roots. This is why the trick of inverting coefficients works for  = 1/x) -- it's a shortcut to replacing all
-- it's a shortcut to replacing all  terms with
terms with 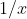 and multiplying out the resulting fractions.
and multiplying out the resulting fractions.
When) isn't monotonic (meaning
isn't monotonic (meaning 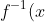) is not a function), it still works; I'm pretty sure you can choose a maximal interval on its domain over which it's monotonic (probably the wrong terminology) and use that for the inverse, because the only necessity is that
is not a function), it still works; I'm pretty sure you can choose a maximal interval on its domain over which it's monotonic (probably the wrong terminology) and use that for the inverse, because the only necessity is that 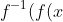) = x) . Also, I'm not convinced that all equations generated in this manner can be manipulated into polynomials without creating new roots (for example, I had some trouble doing it with Sy's question, but I could have just messed up the algebra). Perhaps someone else will have more luck investigating this?
. Also, I'm not convinced that all equations generated in this manner can be manipulated into polynomials without creating new roots (for example, I had some trouble doing it with Sy's question, but I could have just messed up the algebra). Perhaps someone else will have more luck investigating this?
I was playing around with these sorts of problems on the bus the other day, but I ended up confusing myself and didn't get very far.
Say you had a polynomial with roots
You can find an equation with these roots by replacing every instance of
When
- Status
- Not open for further replies.

