Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2016 Integration Marathon
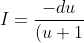\sqrt{u^2+1}} = \frac{1}{2}\int ({\frac{u-1}{\sqrt{u^2+1}} - \frac{\sqrt{u^2+1}}{u+1}})du)
Yeah don't ask...
LOLHow did you p.f. it?
Yeah don't ask...
Last edited:


