-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
MATH1251 Questions HELP (1 Viewer)
- Thread starter 1008
- Start date
Setting up the ODE problem again
I have a feeling that the last two sentences are just making it an IVP problem. But yeah based off the first sentence can someone please tell me where they got this from?
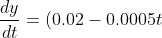y)
Oh alright, that makes sense then...It approaches K. leehuan typoed the solution, it should be +y0 in the denominator. (To see this, note that if we sub. in t = 0, we are supposed to get y = y0.)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Lol even my tutor reckons that question has been typo-d.Got another ODE:

_______________________
I was just wondering, is it possible to apply least squares on this problem?
(I don't mind if no attempt is actually made at this question, with or without lssq)
Last edited:
boredofstudiesuser1
Active Member
- Joined
- Aug 1, 2016
- Messages
- 567
- Gender
- Undisclosed
- HSC
- 2018
What year of maths is this?
Lol even my tutor reckons that question has been typo-d.
_______________________
I was just wondering, is it possible to apply least squares on this problem?
(I don't mind if no attempt is actually made at this question, with or without lssq)
https://en.wikipedia.org/wiki/Least_squares .)
Further info on non-linear least squares, including what the 'normal equations' are in the non-linear case: https://en.wikipedia.org/wiki/Non-linear_least_squares .
Linear least-squares: https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics) .
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Makes sense  I was thinking along the lines of the residual.
I was thinking along the lines of the residual.
______________
I think I just need more guidance with modelling. Solving ODEs aren't too hard in general.


(y is the volume of pollutant after time t days)
edit: resolved by Paradoxica through private conversation
______________
I think I just need more guidance with modelling. Solving ODEs aren't too hard in general.
(y is the volume of pollutant after time t days)
edit: resolved by Paradoxica through private conversation
Last edited:
First year lol (MATH1251 at UNSW)What year of maths is this?
Thanks for that. Yeah, it's probably just easier to not use the substitution and just solve it like a second order ODE.
https://en.wikipedia.org/wiki/Least_squares .)
Further info on non-linear least squares, including what the 'normal equations' are in the non-linear case: https://en.wikipedia.org/wiki/Non-linear_least_squares .
Linear least-squares: https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics) .
boredofstudiesuser1
Active Member
- Joined
- Aug 1, 2016
- Messages
- 567
- Gender
- Undisclosed
- HSC
- 2018
Wow... I'm screwed... what degree would you have to do this in?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Also to the people actually in the course, I'm just helping advertise the PASS classes that they are running. They are worth going imo though.
This question seems pretty tedious to write out (as in, both the qn and ans). I was gonna work my way up by finding m0=f(t) but then I realised that if I did that then I'd be solving an endless stream of first order linear ODEs without guaranteeing I get a pattern. Is there a way to force the pattern out?

This question seems pretty tedious to write out (as in, both the qn and ans). I was gonna work my way up by finding m0=f(t) but then I realised that if I did that then I'd be solving an endless stream of first order linear ODEs without guaranteeing I get a pattern. Is there a way to force the pattern out?

RenegadeMx
Kosovo is Serbian
- Joined
- May 6, 2014
- Messages
- 1,301
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2016
trying to get on the exec team eh?Also to the people actually in the course, I'm just helping advertise the PASS classes that they are running. They are worth going imo though.
This question seems pretty tedious to write out (as in, both the qn and ans). I was gonna work my way up by finding m0=f(t) but then I realised that if I did that then I'd be solving an endless stream of first order linear ODEs without guaranteeing I get a pattern. Is there a way to force the pattern out?

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
I couldn't find this question anywhere in the course pack. Which question is it?I've got another ODE too. Use the substitution to solve:
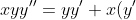^2;u=y'/y \text{ or }u=\ln y)
That is not exact. And it's definitely not linear. But I don't see how it's separable.
And I've lost my motivation to continue.
Edit: Wait
This technically is first order linear, but my last two substitutions do no effect overall. So I'm inclined to think I might've made a mistake
Maybetrying to get on the exec team eh?
Last edited:
Paradoxica
-insert title here-
I didn't use the substitution but that's just moi....I've got a couple of ODEs too.
1)Use the substitution to solve:
 Suppose that }\alpha(x)\text{ is a solution to the equation }\\ \frac{\mathrm{d^2} u}{\mathrm{d} x^2} +b(x) \frac{\mathrm{d} u}{\mathrm{d} x} +c(x)u=0\\\text{(a) Use the substitution }u(x)=\alpha(x)v(x)\text{ to write down a first order equation for } \frac{\mathrm{d} v}{\mathrm{d} x}\\\text{What method can you see to solve this equation?}\\\text{(b) Verify that }u(x)=x^3\text{ is one of the solutions to the differential equation }\\x^2\frac{\mathrm{d^2} u}{\mathrm{d} x^2}-4x\frac{\mathrm{d} u}{\mathrm{d} x}+6u=0\\\text{Hence use the technique of (a) to find the general solution.})
Last edited:
I've got a couple of ODEs too.
1)Use the substitution to solve:
 Suppose that }\alpha(x)\text{ is a solution to the equation }\\ \frac{\mathrm{d^2} u}{\mathrm{d} x^2} +b(x) \frac{\mathrm{d} u}{\mathrm{d} x} +c(x)u=0\\\text{(a) Use the substitution }u(x)=\alpha(x)v(x)\text{ to write down a first order equation for } \frac{\mathrm{d} v}{\mathrm{d} x}\\\text{What method can you see to solve this equation?}\\\text{(b) Verify that }u(x)=x^3\text{ is one of the solutions to the differential equation }\\x^2\frac{\mathrm{d^2} u}{\mathrm{d} x^2}-4x\frac{\mathrm{d} u}{\mathrm{d} x}+6u=0\\\text{Hence use the technique of (a) to find the general solution.})
Yeah it's a weird question...I tried both the substitutions suggested but failed to get to a solution.I couldn't find this question anywhere in the course pack. Which question is it?
That is not exact. And it's definitely not linear. But I don't see how it's separable.
And I've lost my motivation to continue.
Edit: Wait
This technically is first order linear, but my last two substitutions do no effect overall. So I'm inclined to think I might've made a mistake
Maybe
Did you have a look at this one? I added it later on...
Woah.I didn't use the substitution but that's just moi....
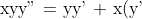^2 $ (divide both sides by $xyy'$)$ \\\\ \frac{y''}{y'} = \frac{1}{x} + \frac{y'}{y} \\ $Integrate both sides with respect to $x$ to obtain:$ \\\\ \log{y'} + \mathcal{C} = \log{x} + \log{y} \\\\ ky' = xy \\ \frac{y'}{y} = k_1 x \\ \log{y} + \mathcal{C}_1 = k_2 x^2)
Wait: if we integrate both sides wrt x, don't we treat y as a constant?
Paradoxica
-insert title here-
No. y is a function of x... Hence, thereby, the thing follows...Woah.
Wait: if we integrate both sides wrt x, don't we treat y as a constant?
Yeah thanks for clarifying that. By doing waay too many exact ODEs (treating y as constant) I completely forgot about that fact.No. y is a function of x... Hence, thereby, the thing follows...
Any thoughts on the other question though?

