Last edited:
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
MATH1251 Questions HELP (1 Viewer)
- Thread starter 1008
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Didn't your tutor go over that one with you?Hey everyone, I've got another question:
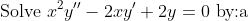 letting }x=e^t\\\text{b) letting }y=x^m)
And the other one just gives you a new characteristic equation in m
No he didn'tDidn't your tutor go over that one with you?
And the other one just gives you a new characteristic equation in m
Wait, how'd you do the implicit diff part?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
d/dx ...No he didn't
Wait, how'd you do the implicit diff part?
= d/dt ... * dt/dx
and dt/dx = exp(-t)
(Recall that implicit differentiation is just a fancy application of the chain rule)
Thanksd/dx ...
= d/dt ... * dt/dx
and dt/dx = exp(-t)
(Recall that implicit differentiation is just a fancy application of the chain rule)
Paradoxica
-insert title here-
No.
Example: a_n = 1/n, b_n = log(1+1/n)
sum (a_n - b_n) = γ (EulerGamma)
but sum (a_n) = ∞
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Not that I know what EulerGamma is but good enough, thanks.No.
Example: a_n = 1/n, b_n = log(1+1/n)
sum (a_n - b_n) = γ (EulerGamma)
but sum (a_n) = ∞
_______________________________________________
They rearrange it into this and just say oh the latter sum is divergent so it must be divergent. Is this, on the other hand, acceptable?
Paradoxica
-insert title here-
I don't think that's valid reasoning. What you can do is show the former sum converges [it does converge, by the comparison test with Zeta(½)], and the latter diverges.
Here's some hints.I had another question:
I get (a), but nothing else...
Thanks! Just a few queries:Here's some hints.
 The limit is the \textsl{Golden Ratio} $\varphi = \frac{1 + \sqrt{5}}{2}$.$)
(b) can we directly state that
(c) I get the logic, but is that all I need to write for c? if not, what do I need to prove?
(d) What is the Monotone Convergence Theorem?
(e) Wow, never knew about the Golden Ratio!
Thanks! Just a few queries:
(b) can we directly state thatfor all n, even though there is a condition in (a) that x has to be between 1 and 2 (inclusive)
(c) I get the logic, but is that all I need to write for c? if not, what do I need to prove?
(d) What is the Monotone Convergence Theorem?
(e) Wow, never knew about the Golden Ratio!
Last edited:
Thanks so much! Btw, how'd you know the limit in (e) was the Golden Ratio? Is it just a property of the ratio, or is there a rule/theorem attached to this?
It's a famous property of the Golden Ratio (which is a famous number with many interesting properties and also appears in nature a lot apparently. See the Wikipedia page: https://en.wikipedia.org/wiki/Golden_ratio ).Thanks so much! Btw, how'd you know the limit in (e) was the Golden Ratio? Is it just a property of the ratio, or is there a rule/theorem attached to this?
I just commented it was the Golden Ratio because I thought some readers may be interested to hear that, you don't actually need to know that to do that Q. Here's how to do it (and how you should do it):
Thanks again, but yeah reading about the Golden Ratio, it is quite unique....It's a famous property of the Golden Ratio (which is a famous number with many interesting properties and also appears in nature a lot apparently. See the Wikipedia page: https://en.wikipedia.org/wiki/Golden_ratio ).
I just commented it was the Golden Ratio because I thought some readers may be interested to hear that, you don't actually need to know that to do that Q. Here's how to do it (and how you should do it):
. So $L^2 - L -1 = 0 \Rightarrow L = \frac{1+\sqrt{5}}{2}$ (taking the positive root since the sequence is positive).$)
Anyway, finally get the general approach for such questions, thanks to the process just posted (I guess I was kinda overwhelmed by the trivial roots inside the roots thing that they gave at the end. I know it's an equivalent way of writing it, but it's trivial to the question)
Maybe the reason they wrote the square roots thing is just so that people doing the Q. would realise they're finding the limit of that. Some students might not have noticed otherwise and would think they're just finding the limit of a random sequence and forget about it quickly.Thanks again, but yeah reading about the Golden Ratio, it is quite unique....
Anyway, finally get the general approach for such questions, thanks to the process just posted (I guess I was kinda overwhelmed by the trivial roots inside the roots thing that they gave at the end. I know it's an equivalent way of writing it, but it's trivial to the question)
I think in highschool they sometimes do Q's like this (like find value of sqrt(1+sqrt(1+…)), where the method used is call that expression x, then get x = sqrt(1+x), and solve for x). But usually in high school for these Q's, they don't prove the limit exists in the first place, which means they don't justify why we can call that expression x in the first place (so they implicitly assume without proof that it's safe to do so).
Last edited:
Yeah I've noticed that too, but what surprised me the most was that some of these assumptions seep into the actual HSC exam too. This is why in HSC, students that may be aware of such facts may find it logically challenging to solve problems by riding on such assumptions, where they fail to draw the line between what is safe to assume and what isn't. I guess tho HSC (3/4unit) is more about just rigorously improving your maths skills by maximising your exposure to questions so that you're able to tackle problems such as this conceptually by basing your responses on that extensive practice you've had in the past.Maybe the reason they wrote the square roots thing is just so that people doing the Q. would realise they're finding the limit of that. Some students might not have noticed otherwise and would think they're just finding the limit of a random sequence and forget about it quickly.
I think in highschool they sometimes do Q's like this (like find value of sqrt(1+sqrt(1+…)), where the method used is call that expression x, then get x = sqrt(1+x), and solve for x. But usually in high school for these Q's, they don't prove the limit exists in the first place, which means they don't justify why we can call that expression x in the first place (so they implicitly assume without proof that it's safe to do so).
PS: You may be right about the reason they wrote the square roots thing.
Last edited:

