Paradoxica
-insert title here-
Re: Several Variable Calculus
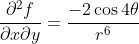
It is then immediately obvious that the limit does not exist as r tends towards zero.
If we switch to polar co-ordinates, then the result is:Just a brief sketch-out please
I know that f is not continuous at 0 but I'm not sure if that helps since we're talking about partial derivatives here.
It is then immediately obvious that the limit does not exist as r tends towards zero.
Last edited:

