(Stats is done for this sem)
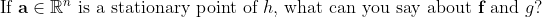
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MATH2111 Higher Several Variable Calculus (1 Viewer)
- Thread starter leehuan
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Chain rule was what was on my mind, but I was getting lost at how to use it
I also started doubting myself, questioning if it's meant to be a Jacobian or just h-dash.
Unless, the answer is just that Jh(a) = 0 so RHS = 0 as well
Edit: Uh, nvm, found a gap in my learning.
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Found it really hard to work around the wording for this question. Not sure how to properly use the implicit function theorem.

Not too sure what exactly they want for my matrices (A|B) either

Not too sure what exactly they want for my matrices (A|B) either
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
What was your end answer?Edit: Uh, nvm, found a gap in my learning.
RenegadeMx
Kosovo is Serbian
- Joined
- May 6, 2014
- Messages
- 1,301
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2016
lel gl with calculus, most aids course(Stats is done for this sem)
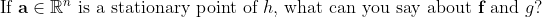
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
I thought I had it but I probably didn't. Not sure what I could possibly do next afterWhat was your end answer?
I really don't feel like that should be the final answer either. Any further guidance?
dyinglel gl with calculus, most aids course
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Idk what they want you to say with that wording and those assumptions really. Basically it just means that the image of f'(a) is a subspace of the kernel of g'(f(a)), or equivalently that the image of f'(a) is orthogonal to the gradient vector of g at f(a).I thought I had it but I probably didn't. Not sure what I could possibly do next after
I really don't feel like that should be the final answer either. Any further guidance?
What have you tried so far? Did you try maybe considering the inverse function theorem?Figures, should've thought in that direction
_______________________
\neq 0.\, \text{Can we conclude that }\\\textbf{f}(\textbf{a})\text{ is an interior point of }\textbf{f}(U)?)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
That was definitely the starting point, but that just asserted that there exists an open setWhat have you tried so far? Did you try maybe considering the inverse function theorem?
Image of an open set under a continuous function might not be open
Generally this is correct, but consider the implications of f being an invertible (locally) continuous map.Image of an open set under a continuous function might not be open
Also, if V is a subset of U, then f(V) is automatically a subset of f(U) (true for any function and sets (that make sense)).That was definitely the starting point, but that just asserted that there exists an open setthat is open, not
right?
(Or maybe you meant that it doesn't state that f(V) is open.)
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Yeah the latter lolAlso, if V is a subset of U, then f(V) is automatically a subset of f(U) (true for any function and sets (that make sense)).
(Or maybe you meant that it doesn't state that f(V) is open.)
________________________________
Just a yes or no answer please because I can't just tell what to use immediately. I know that it converges pointwise to the zero function.
Because seeing as though it converges pointwise to something continuous I doubt I can use that, and the Weierstrass M-test doesn't even seem relevant.
NoYeah the latter lol
________________________________
Just a yes or no answer please because I can't just tell what to use immediately. I know that it converges pointwise to the zero function.
Because seeing as though it converges pointwise to something continuous I doubt I can use that, and the Weierstrass M-test doesn't even seem relevant.
Also the first term on your RHS has a mistake/typo (shouldn't have y).
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014

