ok thanksThats as simple as it gets I think (you can usually simplify if the inverse is in the brackets) also try using \cos^{-1}(x) to getimo looks a lot better
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MX2 Integration Marathon (1 Viewer)
- Thread starter dan964
- Start date
lmao is the answer 0? If not, I screwed upReally cool integral from stanford which a lot of people have probably seen before:
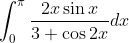
yeplmao is the answer 0
its not i think
wait let me see my mistaleThe answer is: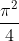
The graph on desmos looks like 0?The answer is: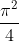
OH IM SUCH A DUMB POO I WAS LITERALLY ATThe answer is: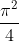
the sin turns to 0 because its odd
and when i did the upper and lower bounds on (pi/2)u i plused not minused pls guys i swear im not crap
Wasn't that in MIt integration bee as well?The answer is: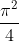
Suffering latex pain I cOH IM SUCH A DUMB POO I WAS LITERALLY AT}du)
idekkedi
Member
- Joined
- Feb 1, 2021
- Messages
- 32
- Gender
- Male
- HSC
- 2021
Sexier than you will ever be.mmm yes sexy latex completed
Directrix
Forklift Certified
- Joined
- May 25, 2020
- Messages
- 322
- Gender
- Undisclosed
- HSC
- 2021
Really cool integral from stanford which a lot of people have probably seen before:
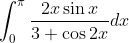
Last edited:
Or we can use the king Rule:Really cool integral from stanford which a lot of people have probably seen before:
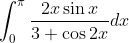
Add 1 and 2 to get:
Exactly how I would have done it. Great minds think alike!Or we can use the king Rule:
(1)
 \sin{x}}{3+\cos{2x}} dx \quad \text{by letting} \quad u=\pi-x)
(2)
Add 1 and 2 to get:

ik this trick is too advanced for me but pls explain the last step to inverse tan cosOr we can use the king Rule:
(1)
(2)
Add 1 and 2 to get:

OH WAIT IM SPECIAL DONT WORRY LOL
So it's jsut using the resultik this trick is too advanced for me but pls explain the last step to inverse tan cos

